Confira aqui um super resumo, simples e objetivo, sobre Análise Combinatória, conteúdo muito explorado em concursos públicos.
Por ser muito extenso, no decorrer do texto existem links para posts específicos sobre cada um dos assuntos.
Bom estudo!
Introdução
A Análise Combinatória é a parte da matemática que estuda a contagem de elementos, possibilidades e combinações de determinados conjuntos. Vejamos um exemplo onde utilizamos tais conceitos:
Exemplo 1. Juliete vai a uma festa e está em dúvida entre duas calças (azul ou vermelha) e três blusas (amarela, preta ou branca). De quantos modos distintos Juliete pode se vestir?
Temos as seguintes opções:
– calça azul e blusa amarela;
– calça azul e blusa preta;
– calça azul e blusa branca;
– calça vermelha e blusa amarela;
– calça vermelha e blusa preta;
– calça vermelha e blusa branca;
Assim, para calcularmos a quantidade de possibilidades que Juliete tem, basta multiplicarmos 2 x 3 = 6 possibilidades.
Princípio Fundamental da Contagem (PFC)
Na análise combinatória, este princípio generaliza o exemplo acima. Sempre que tivermos uma ação constituída de duas etapas, onde a primeira possui m possibilidades e a segunda possui n possibilidades, o número total de possibilidades será m x n. Veja alguns exemplos:
Exemplo 2. Existem 4 estradas ligando as cidades de Linhares e Colatina e 3 estradas ligando Colatina e Vitoria. De quantas maneiras diferentes é possível ir de Linhares a Vitória, passando por Colatina?
Temos:
4 caminhos diferentes para o percurso Linhares x Colatina.
3 caminhos diferentes para o percurso Colatina x Vitória
Pelo PFC temos 4 x 3 = 12
Ou seja, temos 12 caminhos distintos para o percurso Linhares x Vitória.
Exemplo 3. Jennifer possui 6 blusas, 4 saias e 3 sandálias. Quantas combinações diferentes ela pode fazer?
Pelo PFC temos 6 x 4 x 3 = 72
Daí, Jennifer pode se vestir de 72 jeitos diferentes.
Caso queira estudar mais sobre o PFC, clique nos links abaixo:
Princípio Fundamental da Contagem
Exercícios resolvidos sobre o PFC
Fatorial de um número natural
Sendo “n” um número natural, definimos o fatorial de “n”, simbolizado por “n!”, da seguinte forma:
a) 0! = 1
b) 1! = 1
c) n! = n . (n-1) … 3 . 2 . 1 (n diferente de 0 e 1)
Exemplo 4:
4! = 4.3.2.1 = 24
Exemplo 5:
6! = 6.5.4.3.2.1 = 720
Clique nos links abaixo para saber mais sobre o fatorial:
Exercícios resolvidos sobre fatorial
Arranjos
Na análise combinatória, arranjos são agrupamentos dos elementos de um conjunto finito, onde a ordem faz toda a diferença. Veja o exemplo:
Exemplo 6. Seja o conjunto {1, 2, 3, 4, 5}, vamos listar todos os pontos cartesianos que podem ser formados a partir deste conjunto. Veja:
(1, 2); (1, 3); (1, 4); (1, 5);
(2, 1); (2, 3); (2, 4); (2, 5);
(3, 1); (3, 2); (3, 4); (3, 5);
(4, 1); (4, 2); (4, 3); (4, 5);
(5, 1); (5, 2); (5, 3); (5, 4).
Note que temos um conjunto com 5 elementos, que serão tomados dois a dois, e sabendo que a ordem faz toda a diferença, ou seja, estamos considerando (1, 2) diferente de (2, 1). Neste caso podemos calcular o número de arranjos da seguinte forma:
Generalizando, para um arranjo de n elementos, tomados k a k, temos que:
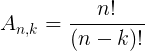
Para saber mais sobre os arranjos clique nos links abaixo:
Exercícios resolvidos sobre arranjos
Permutações
Na análise combinatória, denominamos permutação de n elementos a todo arranjo de n elementos, tomados n a n.
Temos dois casos a considerar:
- Todos os elementos do conjunto são distintos
- Existem elementos repetidos no conjunto
Vamos estudar cada um deles.
- De elementos distintos
Quando temos uma permutação de elementos distintos, podemos calcular a quantidade de permutações através da seguinte fórmula:
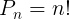
Exemplo 7. Vamos escrever todos os anagramas que podem ser escritos pelas letras ABC:
ABC, ACB, BAC, BCA, CAB, CBA
Note que o exemplo foi escolhido devido a simplicidade. Em casos mais complexos é inviável listar todas as possibilidades.
Vamos utilizar a fórmula para calcular a quantidade de permutações das letras ABC:
Pn = n!
P3 = 3!
P3 = 3.2.1
P3 = 6
- Com elementos repetidos
Quando temos uma permutação com elementos distintos, onde cada uma das repetições acontece na quantidade n1, n2, …, nt, podemos calcular a quantidade de permutações através da seguinte fórmula:
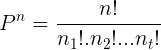
Exemplo 8. Vamos escrever todos os anagramas que podem ser escritos pelas letras da palavra CAPA:
CAPA, CAAP, CPAA, ACPA, APCA, APAC, ACAP, AACP, AAPC, PCAA, PACA, PAAC
Note que listamos 12 anagramas. Se todas as letras fossem distintas listaríamos 24. A diminuição deve-se ao fato da letra A aparecer duas vezes.
Exemplo 9. Quantidade de anagramas que podem ser formados a partir da palavra SOSSEGADO:
Devemos observar que a letra S aparece 3 vezes e a letra O aparece duas vezes.
P9 = 9! / 3!.2! = 30240
Para saber mais sobre permutações e anagramas clique nos links abaixo:
Permutação de elementos distintos
Exercícios resolvidos sobre anagramas
Combinações
Na análise combinatória, combinações são agrupamentos dos elementos de um conjunto finito com n elementos, tomados k a k, onde a ordem é irrelevante.
Podemos calcular a quantidade de combinações através da seguinte fórmula:
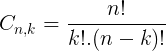
Exemplo 10. Seja o conjunto A = {1, 2, 3, 4, 5}, vamos listar todos os subconjuntos formados por 2 elementos de A:
(1, 2); (1, 3); (1, 4); (1, 5); (2, 3); (2, 4); (2, 5); (3, 4); (3, 5); (4, 5).
Note que estamos considerando (1, 2) igual a (2, 1). Neste caso, o número de combinações será calculado da seguinte forma:
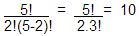
Clique nos links abaixo para saber mais sobre as combinações:
Exercícios resolvidos sobre combinações
Gostou da nossa publicação sobre Análise Combinatória?
Deixe o seu comentário.

Obrigado!
Excelente material. Consegui enender melhor por aqui.
até.