Continuando o estudo da Análise Combinatória, veremos aqui o a definição de fatorial, como calcular e vários exemplos.

Bom estudo!

Definição

Dado um número natural n, definimos o fatorial de n (simbolizado por n!) através da seguintes relações:

• Fatorial de n:

n! = n . (n-1) . (n-2) … 4 . 3 . 2 . 1, para n≥2

• Fatorial de 1:

1! = 1

• Fatorial de 0:

0! = 1

Como pode ser observado, a definição é bem simples. O fatorial de um número maior ou igual a 2 é o produto dos números naturais de 1 até n. Já para os números 0 e 1, existe uma definição especial, onde o fatorial é igual a 1.

Exemplo. Fatorial de 5:

5! = 5.4.3.2.1 = 120

Muito simples não é mesmo? Confira abaixo a lista dos fatoriais de 0 a 10:

0! = 1

1! = 1

2! = 2.1 = 1

3! = 3.2.1 = 6

4! = 4.3.2.1 = 24

5! = 5.4.3.2.1 = 240

6! = 6.5.4.3.2.1 = 720

7! = 7.6.5.4.3.2.1 = 5.040

8! = 8.7.6.5.4.3.2.1 = 40.320

9! = 9.8.7.6.5.4.3.2.1 = 362.880

10! = 10.9.8.7.6.5.4.3.2.1 = 3.628.800

Simplificando frações com fatorial

Quando utilizamos o fatorial em frações é possível efetuarmos algumas simplificações, de modo a facilitar os nossos cálculos. Veja:

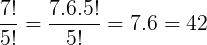
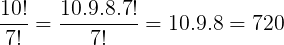
Gostou da nossa publicação sobre fatorial?

Deixe o seu comentário.