Dando continuidade ao estudo da temida Análise Combinatória, nesta página falaremos sobre os Arranjos Simples.
O assunto é bem complexo e pode ser muito explorado em provas de concursos e vestibulares, por isso vale a pena estudar bastante o conteúdo.
Lembrando que existem dois tipos de arranjos, os arranjos simples e os arranjos com repetição.
Bom estudo!
O que são arranjos simples?
Arranjos simples são agrupamentos dos elementos de um conjunto finito, onde a ordem faz toda a diferença, e não há repetição.
Exemplo 1:
Seja o conjunto W = {1, 2, 3, 4}. Vamos escrever todos os números de dois algarismos que podem ser formados com os elementos do conjunto W, sem repetição de algarismos:
12, 13, 14,
21, 23, 24
31, 32, 34
41, 42, 43
Nota-se que foram formados 12 números distintos a partir de um conjunto com quatro algarismos, tomados dois a dois, sem repetição.
Outro ponto a ser observado é que 12 ≠ 21, que conforme já citado, nos arranjos a ordem dos elementos faz toda a diferença.
Definição Formal
Dado um conjunto com uma quantidade n de elementos distintos, chamamos de arranjo simples dos n elementos, tomados k a k, a qualquer sequência ordenada de k elementos distintos escolhidos entre os n elementos deste conjunto.
Analisando o exemplo do conjunto W = {1, 2, 3, 4}, temos n = 4 e k = 2.
Fórmula para cálculo do número de arranjos simples
O exemplo estudado até agora foi escolhido por ser bem simples e ideal para introduzir o conteúdo, porém existem casos onde listar os arranjos poderia demorar horas, ou até dias… Para facilitar, vamos aprender a utilizar a fórmula para calcular o número de arranjos simples. Veja:
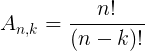
Onde:
An,k = quantidade de arranjos
n = quantidade de elementos do conjunto
k = quantidade de elementos por arranjo
n ≥ k
Exemplo 2. Quantos arranjos de três letras podem ser formados através do conjunto A = {E, I, O, U}?
O primeiro passo é observar que o conjunto tem 4 elementos e que cada arranjo será formado por 3 deles. Ou seja, n = 4 e k = 3.
Utilizando a fórmula:
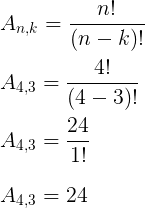
Exemplo 3. Quantas “palavras” (com ou sem sentido) de 6 letras distintas podem ser formadas com as letras A, B, C, D, E, F, G, H, I, e J?
Claramente trata-se de um problema de análise combinatória, mais especificamente de arranjos.
Temos que n = 10 e k = 6.
Utilizando a fórmula:
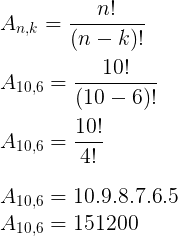
Gostou da nossa publicação sobre arranjos simples?
Deixe o seu comentário.

Pingback: ANÁLISE COMBINATÓRIA – RESUMO – Saber Matemática
Por que o Exemplo 3 não e permutação simples de anagrama ??? obrigado pela atenção!
Teo,
Porque apenas parte das letras serão escolhidas.