Dando continuidade ao estudo da Análise Combinatória, vamos aprender a calcular a quantidade de anagramas de palavras.
Pede-se que o aluno tenha conhecimentos acerca do fatorial de um número natural e do Princípio Fundamental da Contagem.
Bom estudo!
Definição
Calcular a quantidade de anagramas de uma palavra é calcular quantas “palavras”, com ou sem sentido, podemos escrever com as letras utilizadas para escrevê-la.
Como exemplo, podemos listar os 6 anagramas da palavra GOL.
Exemplo 1. Anagramas da palavra GOL:
GOL, GLO, OGL, OLG, LGO, LOG
Calcular a quantidade de anagramas de uma palavra com apenas 3 letras é muito fácil. Vamos agora aprender um método simples e viável para o caso de palavras com muitas letras.
Temos dois casos a considerar:
- Palavras com letras diferentes
- Palavras com letras repetidas
Anagramas de palavras com letras diferentes
Para calcular a quantidade de anagramas de uma palavra com letras diferentes, basta utilizarmos o princípio fundamental da contagem. Veja o exemplo:
Exemplo 2. Calcular a quantidade de anagramas da palavra LIVRO:
Precisamos utilizar as 5 letras para escrevermos várias “palavras” diferentes:
_ _ _ _ _
Temos:
5 opções para a primeira posição
4 opções para a segunda posição
3 opções para a terceira posição
2 opções para a quarta posição
1 opção para a última posição
Ou seja, a quantidade de anagramas da palavra LIVRO é:
5.4.3.2.1 = 120
O fato da quantidade de anagramas de uma palavra com 5 letras distintas ser igual a 5! não é coincidência. Para calcularmos a quantidade de anagramas de uma palavra com letras distintas, basta calcularmos o fatorial do número que representa a quantidade de letras.
Exemplo 3. Quantidade de anagramas da palavra AMOR:
4! = 4.3.2.1 = 24
Exemplo 4. Quantidade de anagramas da palavra MULHER:
6! = 6.5.4.3.2.1 = 720
Exemplo 5. Quantidade de anagramas da palavra FUTEBOL:
7! = 7.6.5.4.3.2.1 = 5040
Anagramas de palavras com letras repetidas
Agora que já aprendemos a calcular a quantidade de anagramas com letras distintas, vamos aprender a calcular quando a palavra apresenta letras repetidas. O cálculo é muito simples, basta contar a quantidade de repetições.
Veja o exemplo:
Exemplo 6. Calcular a quantidade de anagramas da palavra JABUTICABA.
Temos 10 letras. Se todas fossem diferentes, a quantidade de anagramas seria igual a 10!. Mas não é tão simples assim pois temos algumas repetições:
- A letra A aparece 3 vezes
- A letra B aparece 2 vezes
Devemos descontar as repetições para que a contagem dos anagramas seja feita da forma correta. Para que isto seja feito, vamos dividir o 10! pelo fatorial de cada uma das repetições. Veja:
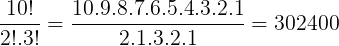
Veja que:
10! – representa a quantidade total de palavras
3! – representa a quantidade de vezes que a letra A aparece
2! – representa a quantidade de vezes que a letra B aparece
Exemplo 7. Calcular a quantidade de anagramas da palavra MATEMATICA.
Temos:
Quantidade de letras: 10
Quantidade de vezes que a letra M aparece: 2
Quantidade de vezes que a letra A aparece: 3
Quantidade de vezes que a letra T aparece: 2
Calculando:
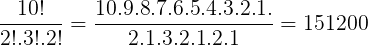
Exemplo 8. Calcular a quantidade de anagramas da palavra ABACATE.
Temos:
Quantidade de letras: 7
Quantidade de vezes que a letra A aparece: 3
Calculando:
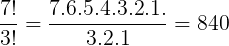
Gostou da nossa publicação sobre anagramas?
Deixe o seu comentário.

Pingback: ANÁLISE COMBINATÓRIA – RESUMO – Saber Matemática
Bom dia! No exemplo 7, não entendi como é realizado o calculo dos denominadores.
Neiva
Olá Maria!
Nós calculamos o fatorial:
3! = 3.2.1
2! = 2.1
Obrigada pela explicação, ajudou bastante!!! 🙂
Como fazer a seguinte questao.
Todos os Anagrama possiveis da palavra CANTAGALO
Qual a probabilidade de eu tirar ao acaso os anagramas iniciados com “CANTA”, ou seja, as 4 ultimas letras (g, a, l, o) podem estar em qualquer ordem.
Essa explicação ajudou muito mas sabe como faço combinatória?
Olá Victor!
Sugiro que leia o conteúdo sobre o assunto e estude também através dos exercícios resolvidos.
Muito bom,, me ajudou em uma questão de concurso
Olá Regis,
Fico feliz em ajudar…
Ex. O cálculo de 4 algarismos sem restrições
Sem restrições:
10.10.10.10 = 10000
Paulo escreveu a
palavra CELSO em uma folha de cartolina branca. O
número total de anagramas que podemos formar com essa palavra em que as consoantes aparecem sempre
juntas e em qualquer ordem.
Se não tivesse restrições seria 5!, 120 anagramas. Como as consoantes tem de ficar juntas, as vogais variariam só 2 vezes para cada combinação das 3 consoantes (3!). Então teria 3x2x6=36
para anagrama da palavra constituente por exemplo. tendo duas letras juntas como exemplo sc e ainda tenhp que a primeira ser vogal. como q faz ?
Interessante esse artigo. Muito bem explicado. Gostei.
Isso me ajudou bastante, eu estava meio atrasada com os deveres de matemática, mas foi tão fácil entender quando entrei aqui <3
gostei bastante,tinha dúvidas sobre esse assunto e agora nao tenho mais 🙂
eu queria sabe como que faz anagrama de duas palavras, tipo ¨bom dia¨ ou ¨Harry Potter¨. vou ter uma prova que vai cai isso e eu não sei como faz