PRINCÍPIO FUNDAMENTAL DA CONTAGEM (PFC)

Dando início ao estudo da Análise Combinatória, vamos falar sobre o Principio Fundamental da Contagem, também conhecido como PFC.

Trata-se de um conteúdo relativamente simples e muito explorado em provas de concursos.

Bom estudo!

 

 

SITUAÇÃO PROBLEMA

Alice vai a uma festa de casamento hoje. Ao abrir o guarda roupas ela percebeu que possui 3 vestidos e 4 sandálias apropriadas ao evento. Quantas combinações diferentes podem ser feitas com os vestidos e sandálias à disposição de Alice?

Veja as opções que Alice possui:

Uma observação importante é que não nos cabe analisar se o vestido combina com a sandália (rsrsrs). Nosso papel é apenas calcular a quantidade de combinações possíveis.

 

Calculando:

• Quando Alice escolhe o vestido amarelo ela pode escolher usar uma das 4 sandálias.
• Ao escolher o vestido vermelho, Alice também pode escolher entre as 4 sandálias.
• Da mesma forma, quando Alice escolhe o vestido verde, possui 4 opções para as sandálias.

Desta forma, o total de opções é:

4 + 4 + 4 = 12

 

Uma outra forma de resolver o problema é através do Princípio Fundamental da Contagem (PFC).

Como ela possui 3 vestidos e 4 sandálias, basta efetuar a multiplicação:

3 x 4 = 12

 

 

PFC

O Principio Fundamental da Contagem diz que quando uma ação é composta por duas etapas sucessivas, onde a primeira pode ser realizada de n maneiras distintas, e para cada uma dessas possibilidades, a segunda etapa pode ser realizada de m maneiras distintas, então, o número de possibilidades de se efetuar a ação completa é calculado através do produto m.n.

O mesmo princípio vale para ações constituídas de 3 ou mais etapas sucessivas.

 

 

Exemplo 1.

Há 3 estradas ligando as cidades X e Y, e 5 estradas ligando as cidades Y e Z. De quantas maneiras distintas é possível ir de X a Z, passando por Y?

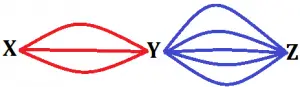
Nota-se que a viagem de X a Z é uma ação composta por duas etapas sucessivas:

Etapa 1: O trajeto de X a Y pode ser feito através de 3 estradas distintas.

Etapa 2: O trajeto de Y a Z pode ser feito através de 5 estradas distintas.

Pelo Princípio Fundamental da Contagem (PFC), a quantidade de maneiras possíveis é:

3 x 5 = 15

 

 

Exemplo 2.

Quantos números de 3 algarismos podem ser formados com os números 2, 4, 5, 6 e 8?

A formação de um número de 3 algarismos, nas condições propostas, é uma ação constituída por três etapas sucessivas.

Etapa 1: Escolher o algarismo das centenas. Temos 5 opções possíveis.

Etapa 2: Escolher o algarismo das dezenas. Temos 4 opções possíveis pois não podemos utilizar o algarismo das centenas.

Etapa 3: Escolher o algarismo das unidades. Temos 3 opções possíveis pois não podemos utilizar os algarismos das centenas nem das dezenas.

Pelo Princípio Fundamental da Contagem, a quantidade de números possíveis é:

5 x 4 x 3 = 60