Exercícios resolvidos: ANAGRAMAS

Confira aqui vários exercícios resolvidos sobre anagramas, um dos tópicos de Análise Combinatória. Recomendamos a leitura prévia dos nossos conteúdos sobre anagramas e fatorial.

Bom estudo!

Questão 1 (Anatel – Cespe – adaptada). Considerando-se que um anagrama da palavra ANATEL seja uma permutação das letras dessa palavra, tendo ou não significado na linguagem comum, que n₁ seja a quantidade de anagramas distintos que é possível formar com essa palavra e n₂ seja a quantidade de anagramas distintos dessa palavra que começam por vogal, então n₂/n₁ é igual a:

a) 1/2

b) 2

c) 1

d) 2/3

e) 3/2

Resolução

Calculando a quantidade de anagramas da palavra ANATEL.

Temos um total de 6 letras e uma repetição da letra A:

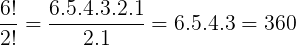
Daí, n₁ = 360

Calculando a quantidade de anagramas da palavra ANATEL que começam por vogal.

Como existe uma repetição da letra A, que é uma vogal, temos dois casos a considerar:

• Caso 1 – Anagramas que começam com a letra A
• Caso 2 – Anagramas que começam com a letra E

Caso 1. Nos casos onde a primeira letra é A, devemos calcular a quantidade de anagramas com as letras restantes, ou seja, calcular a quantidade de anagramas da palavra NATEL.

Como temos um total de 5 letras distintas, podemos calcular da seguinte forma:

5! = 5.4.3.2.1 = 120

Caso 2. Nos casos onde a primeira letra é E, devemos calcular a quantidade de anagramas da palavra ANATL.

Como temos um total de 5 letras, sendo que a letra A se repete, podemos calcular da seguinte forma:

5! / 2! = 5.4.3.2.1 / 2.1 = 60

Daí, n₂ = 120 + 60 = 180

Finalizando,

n₂ / n₁ = 180/360 = 1/2

Resposta: A

Questão 2 (Copel – UFMT). Com as letras da palavra COPEL, a soma do número de anagramas distintos que começam com C com o número de anagramas distintos que começam com C e terminam com L é igual a:

a) 40

b) 35

c) 30

d) 45

Resolução

Calculando a quantidade de anagramas que começam com C:

Basta calcular a quantidade de anagramas da “palavra” OPEL. Como temos 4 letras distintas:

4! = 4.3.2.1 = 24

Calculando a quantidade de anagramas que começam por C e terminam com L:

Basta calcular a quantidade de anagramas da “palavra” OPE. Como temos 3 letras distintas:

3! = 3.2.1 = 6

Finalizando,

24 + 6 = 30

Resposta: C

Questão 3 (Transpetro – Cesgranrio). Qual é o número de anagramas da palavra TRANSPETRO em que as letras PETRO ficam juntas e nessa ordem?

a) 6! / 2!.2!

b) 6!

c) 6!.5!

d) 10! / 2!.2!

e) 10!

Resolução

Sabemos que a palavra TRANSPETRO possui 10 letras, porém o objetivo da questão é que as letras PETRO fiquem juntas e nessa ordem. Para fins de cálculo, vamos considerar que a palavra PETRO é apenas uma letra.

Devemos então calcular a quantidade de anagramas de uma “palavra” com 6 letras (T, R, A, N, S, PETRO).

Conforme visto em nosso material didático, basta calcular o valor de 6!.

Resposta: B

Questão 4 (PM ES – AOCP). Considerando a palavra SOLDADO, é correto afirmar que

(A) é possível formar 360 anagramas dessa palavra que começam pela letra L.

(B) é possível formar 720 anagramas dessa palavra que começam pela letra D.

(C) é possível formar 5040 anagramas dessa palavra, no total.

(D) é possível formar 24 anagramas dessa palavra que começam com a letra D e terminam com a letra O.

(E) é possível formar 12 anagramas dessa palavra que terminam com as letras SOL, nessa ordem.

Resolução

Quantidade de anagramas que começam com a letra L.

L _ _ _ _ _ _ (duas letras D e duas letras O)

6! / 2!2! = 180

Quantidade de anagramas que começam com a letra D.

D _ _ _ _ _ _ (duas letras O)

6! / 2! = 360

Quantidade total de anagramas.

_ _ _ _ _ _ _ (duas letras D e duas letras O)

7! / 2!2! = 1260

Quantidade de anagramas que começam com D e terminam com O.

D _ _ _ _ _ O

5! = 120

Quantidade de anagramas que terminam com SOL.

_ _ _ _ S O L (duas letras D)

4! / 2! = 12

Resposta: E

Questão 5 (PM SP – Vunesp). Considere todos os anagramas da palavra BRASIL.

O número de anagramas que não têm as vogais juntas é

(A) 720.

(B) 600.

(C) 480.

(D) 240.

(E) 120.

Resolução

Considerando que não existem letras repetidas, a quantidade total de anagramas da palavra BRASIL é:

6! = 6.5.4.3.2.1 = 720

Calcularemos a quantidade de anagramas da palavra BRASIL que possuem vogais juntas, considerando que existem apenas duas (A e I).

Considerando AI como apenas uma letra, a quantidade de anagramas será:

5! = 5.4.3.2.1 = 120

Como podemos inverter as duas vogais, ou seja, AI é diferente de IA, temos 240 anagramas da palavra BRASIL com as vogais juntas.

A quantidade de anagramas que não possuem vogais juntas será exatamente a diferença:

720 – 240 = 480

Resposta: C

Questão 6 (TRF – FCC). Um anagrama de uma palavra é obtido trocando-se a ordem de suas letras, não importando se o resultado tem ou não significado em nosso idioma. Colocando em ordem alfabética todos os anagramas da palavra PROVA, a posição ocupada pela palavra PROVA é a

(A) 62a.

(B) 63a.

(C) 64a.

(D) 65a.

(E) 66a.

Resolução

Todos os anagramas que começam com a letra A estão na frente da palavra PROVA.

A _ _ _ _

4 x 3 x 2 x 1 = 24

Todos os anagramas que começam com a letra O estão na frente da palavra PROVA.

O _ _ _ _

4 x 3 x 2 x 1 = 24

Todos os anagramas que começam com PA estão na frente da palavra PROVA.

PA _ _ _

3 x 2 x 1 = 6

Todos os anagramas que começam com PO estão na frente da palavra PROVA.

PO _ _ _

3 x 2 x 1 = 6

Todos os anagramas que começam com PRA estão na frente da palavra PROVA.

PRA _ _

2 × 1 = 2

O anagrama PROAV também está na frente da palavra PROVA.

Total:

24 + 24 + 6 + 6 + 2 + 1 = 63

Posição ocupada pela palavra PROVA: 64a

Resposta: C

Questão 7 (CRM ES – Quadrix). Em um campeonato de futebol, uma vitória corresponde a 3 pontos ganhos, um empate corresponde a 1 ponto ganho e, em caso de derrota, não há pontuação. Após cinco jogos disputados nesse campeonato, de quantas maneiras diferentes um time pode obter exatamente cinco pontos?

a) 3

b) 25

c) 30

d) 5

e) 31

Resolução

Existem duas opções para, nessas condições, um time conseguir 5 pontos em 5 jogos:

• Empatar todos os jogos.
• Ganhar um, empatar dois e perder dois jogos.

Vamos calcular de quantas maneiras a segunda opção pode ocorrer. O que pode ser facilmente calculado através de Anagramas. Veja:

Calculando de quantas sequências diferentes podem ser formadas com as letras V, E, E, D, D, onde V representa vitória, E empate e D derrota.

5! / 2!2! = 120/4 = 30

Como o time tem 30 formas diferentes de conseguir uma vitória, dois empates e duas derrotas, além da outra opção que seria empatar todos os jogos, a quantidade total será 31.

Resposta: E

Gostou dos nossos exercícios resolvidos sobre anagramas?

Deixe o seu comentário.