Dando continuidade ao estudo da análise combinatória, nesta página apresentaremos a permutação simples.
Como em todo conteúdo da análise combinatória, pede-se que o aluno tenha conhecimento prévio sobre fatorial.
Bom estudo!
Permutação simples
Dado um conjunto com n elementos distintos, chamamos de permutação dos n elementos a todo arranjo desses n elementos, tomados n a n, sem repetição.
Para simplificar, permutação é um caso especial de arranjo, onde os n elementos são tomados n a n. Veja:
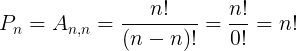
Assim, para calcular a quantidade de permutações simples de um conjunto de n elementos distintos, vamos utilizar a seguinte fórmula:
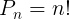
Exemplo 1. De quantas maneiras Ana, Beatriz, Clarice, Débora e Érica podem ser dispostas em uma fila indiana?
Temos que organizar 5 pessoas (diferentes) em uma fila (a ordem importa), ou seja, temos uma permutação simples.
Pn = n!
P5 = 5!
P5 = 5.4.3.2.1
P5 = 120
Exemplo 2. De quantas maneiras 8 pessoas podem se sentar em uma van com a mesma quantidade de lugares?
Calculando a permutação simples, onde n = 8:
Pn = n!
P8 = 8!
P8 = 8.7.6.5.4.3.2.1
P8 = 40320
Exemplo 3. Quantas “palavras”, com ou sem sentido, podem ser escritas a partir das letras A, B, C e D?
Calculando a permutação simples, onde n = 4:
Pn = n!
P4 = 4!
P4 = 4.3.2.1
P4 = 24
Exemplo 4. De quantas maneiras distintas podemos organizar 7 crianças, sendo 4 meninos e 3 meninas, em uma fila indiana:
a) Em qualquer ordem.
Permutação simples de 7 pessoas:
Pn = n!
P7 = 7!
P7 = 7.6.5.4.3.2.1
P7 = 5040
b) Iniciando com uma menina e terminando com um menino.
Como temos 3 meninas, temos 3 opções para iniciarmos a fila.
Como temos 4 meninos, temos 4 opções para terminarmos a fila.
Restaram 5 crianças, onde podemos fazer a permutação simples:
Pn = n!
P5 = 5!
P5 = 5.4.3.2.1
P5 = 120
Calculando o total:
3 x 120 x 4 = 1440
Aprendeu a identificar uma permutação simples?
Deixe o seu comentário.
