Confira aqui a prova resolvida do ENEM 2023. Baseada no caderno amarelo da prova de matemática e suas tecnologias.
Bom estudo!
Questão 136. Alguns estudos comprovam que os carboidratos fornecem energia ao corpo, preservam as proteínas estruturais dos músculos durante a prática de atividade física e ainda dão força para o cérebro coordenar os movimentos, o que de fato tem impacto positivo no desenvolvimento do praticante. O ideal é consumir 1 grama de carboidrato para cada minuto de caminhada.
Um casal realizará diariamente 30 minutos de caminhada, ingerindo, antes dessa atividade, a quantidade ideal de carboidratos recomendada. Para ter o consumo ideal apenas por meio do consumo de pão de fôrma integral, o casal planeja garantir o suprimento de pães para um período de 30 dias ininterruptos. Sabe-se que cada pacote desse pão vem com 18 fatias, e que cada uma delas tem 15 gramas de carboidratos.
A quantidade mínima de pacotes de pão de fôrma necessários para prover o suprimento a esse casal é
A) 1.
B) 4.
C) 6.
D) 7.
E) 8.
Clique aqui para ver a resolução escrita.
Clique aqui para ver a resolução no Youtube.
QUESTÃO 137. O mastro de uma bandeira foi instalado perpendicularmente ao solo em uma região plana. Devido aos fortes ventos, três cabos de aço, de mesmo comprimento, serão instalados para dar sustentação ao mastro. Cada cabo de aço ficará perfeitamente esticado, com uma extremidade num ponto P do mastro, a uma altura h do solo, e a outra extremidade, num ponto no chão, como mostra a figura.
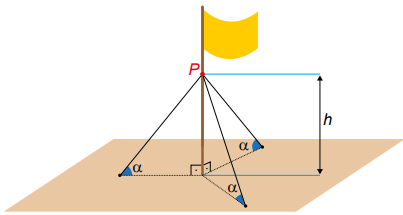
Os cabos de aço formam um ângulo α com o plano do chão.
Por medida de segurança, há apenas três opções de instalação:
- opção I: h = 11 m e α = 30°
- opção II: h = 12 m e α = 45°
- opção III: h = 18 m e α = 60°
A opção a ser escolhida é aquela em que a medida dos cabos seja a menor possível.
Qual será a medida, em metro, de cada um dos cabos a serem instalados?
a) 22√3 / 3
b) 11√2
c) 12√2
d) 12√3
e) 22
Clique aqui para ver a resolução.
QUESTÃO 138. Um controlador de voo dispõe de um instrumento que descreve a altitude de uma aeronave em voo, em função da distância em solo. Essa distância em solo é a medida na horizontal entre o ponto de origem do voo até o ponto que representa a projeção ortogonal da posição da aeronave, em voo, no solo. Essas duas grandezas são dadas numa mesma unidade de medida.
A tela do instrumento representa proporcionalmente as dimensões reais das distâncias associadas ao voo. A figura apresenta a tela do instrumento depois de concluída a viagem de um avião, sendo a medida do lado de cada quadradinho da malha igual a 1 cm.
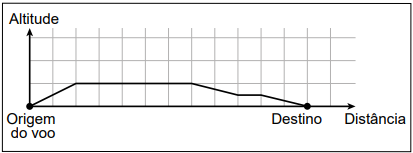
Essa tela apresenta os dados de um voo cuja maior altitude alcançada foi de 5 km.
A escala em que essa tela representa as medidas reais é
A) 1 : 5.
B) 1 : 11.
C) 1 : 55.
D) 1 : 5 000.
E) 1 : 500 000.
Clique aqui para ver a resolução.
QUESTÃO 139. Uma pessoa pratica quatro atividades físicas — caminhar, correr, andar de bicicleta e jogar futebol — como parte de seu programa de emagrecimento. Essas atividades são praticadas semanalmente e acordo com o quadro, que apresenta o número de horas diárias por atividade.
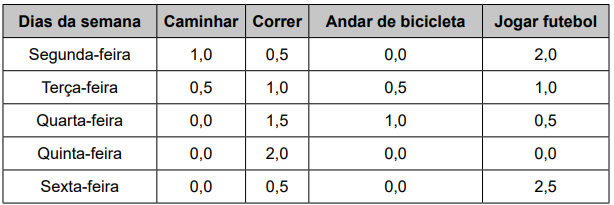
Ela deseja comemorar seu aniversário e escolhe o dia da semana em que o gasto calórico com as atividades físicas praticadas for o maior. Para tanto, considera que os valores dos gastos calóricos das atividades por hora (cal/h) são os seguintes:

O dia da semana em que será comemorado o aniversário é
A) segunda-feira.
B) terça-feira.
C) quarta-feira.
D) quinta-feira.
E) sexta-feira
Clique aqui para ver a resolução.
QUESTÃO 140. A cada bimestre, a diretora de uma escola compra uma quantidade de folhas de papel ofício proporcional ao número de alunos matriculados. No bimestre passado, ela comprou 6 000 folhas para serem utilizadas pelos 1 200 alunos matriculados. Neste bimestre, alguns alunos cancelaram suas matrículas e a escola tem, agora, 1150 alunos.
A diretora só pode gastar R$ 220,00 nessa compra, e sabe que o fornecedor da escola vende as folhas de papel ofício em embalagens de 100 unidades a R$ 4,00 a embalagem. Assim, será preciso convencer o fornecedor a dar um desconto à escola, de modo que seja possível comprar a quantidade total de papel ofício necessária para o bimestre.
O desconto necessário no preço final da compra, em porcentagem, pertence ao intervalo
A) (5,0 ; 5,5).
B) (8,0 ; 8,5).
C) (11,5 ; 12,5).
D) (19,5 ; 20,5).
E) (3,5 ; 4,0).
Clique aqui para ver a resolução.
QUESTÃO 141. O calendário maia apresenta duas contagens simultâneas de anos, o chamado ano Tzolkim, composto por 260 dias e que determinava o calendário religioso, e o ano Haab, composto por 365 dias e que determinava o calendário agrícola. Um historiador encontrou evidências de que gerações de uma mesma família governaram certa comunidade maia pelo período de 20 ciclos, sendo cada ciclo formado por 52 anos Haab.
De acordo com as informações fornecidas, durante quantos anos Tzolkim aquela comunidade maia foi governada por tal família?
A) 741
B) 1 040
C) 1 460
D) 2 100
E) 5 200
Clique aqui para ver a resolução.
QUESTÃO 142. Sejam a, b e c as medidas dos lados de um triângulo retângulo, tendo a como medida da hipotenusa. Esses valores a, b e c são, respectivamente, os diâmetros dos círculos C1, C2 e C3, como apresentados na figura.
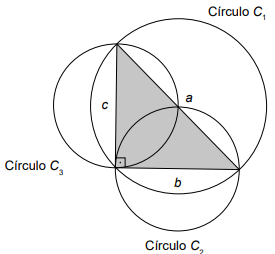
Observe que essa construção assegura, pelo teorema de Pitágoras, que área (C1) = área (C2) + área (C3).
Um professor de matemática era conhecedor dessa construção e, confraternizando com dois amigos em uma pizzaria onde são vendidas pizzas somente em formato de círculo, lançou um desafio: mesmo sem usar um instrumento de medição, poderia afirmar com certeza se a área do círculo correspondente à pizza que ele pedisse era maior, igual ou menor do que a soma das áreas das pizzas dos dois amigos. Assim, foram pedidas três pizzas. O professor as dividiu ao meio e formou um triângulo com os diâmetros das pizzas, conforme indicado na figura.
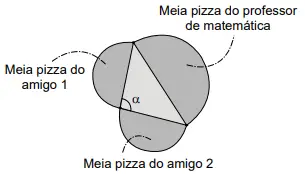
A partir da medida do ângulo α, o professor afirmou que a área de sua pizza é maior do que a soma das áreas das outras duas pizzas.
A área da pizza do professor de matemática é maior do que a soma das áreas das outras duas pizzas, pois
A) 0° < α < 90°
B) α = 90°
C) 90° < α < 180°
D) α = 180°
E) 180° < α < 360°
Clique aqui para ver a resolução.
QUESTÃO 143. Entre maratonistas, um parâmetro utilizado é o de economia de corrida (EC). O valor desse parâmetro é calculado pela razão entre o consumo de oxigênio, em mililitro (mL) por minuto (min), e a massa, em quilograma (kg), do atleta correndo a uma velocidade constante.
Um maratonista, visando melhorar sua performance, auxiliado por um médico, mensura o seu consumo de oxigênio por minuto a velocidade constante. Com base nesse consumo e na massa do atleta, o médico calcula o EC do atleta.
A unidade de medida da grandeza descrita pelo parâmetro EC é
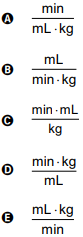
Clique aqui para ver a resolução.
QUESTÃO 144. O gerente de uma fábrica pretende comparar a evolução das vendas de dois produtos similares (I e II). Para isso, passou a verificar o número de unidades vendidas de cada um desses produtos em cada mês. Os resultados dessa verificação, para os meses de abril a junho, são apresentados na tabela.
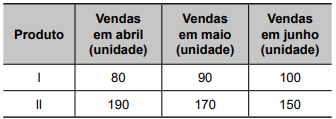
O gerente estava decidido a cessar a produção do produto II no mês seguinte àquele em que as vendas do produto I superassem as do produto II. Suponha que a variação na quantidade de unidades vendidas dos produtos I e II se manteve, mês a mês, como no período representado na tabela.
Em qual mês o produto II parou de ser produzido?
A) Junho.
B) Julho.
C) Agosto.
D) Setembro.
E) Outubro.
Clique aqui para ver a resolução.
QUESTÃO 145. Uma empresa de transporte faz regularmente um levantamento do número de viagens realizadas durante o dia por todos os 160 motoristas cadastrados em seu aplicativo. Em um certo dia, foi gerado um relatório, por meio de um gráfico de barras, no qual se relacionaram a quantidade de motoristas com a quantidade de viagens realizadas até aquele instante do dia.
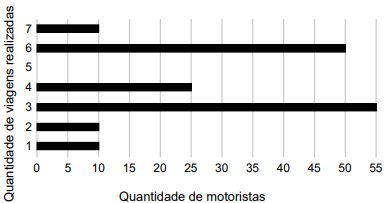
Comparando os valores da média, da mediana e da moda da distribuição das quantidades de viagens realizadas pelos motoristas cadastrados nessa empresa, obtém-se
A) mediana = média < moda.
B) mediana = moda < média.
C) mediana < média < moda.
D) moda < média < mediana.
E) moda < mediana < média.
Clique aqui para ver a resolução.
QUESTÃO 146. A foto mostra a construção de uma cisterna destinada ao armazenamento de água. Uma cisterna como essa, na forma de cilindro circular reto com 3 m² de área da base, foi abastecida por um curso d’água com vazão constante. O seu proprietário registrou a altura do nível da água no interior da cisterna durante o abastecimento em diferentes momentos de um mesmo dia, conforme o quadro.

Qual foi a vazão, em metro cúbico por hora, do curso d’água que abasteceu a cisterna?
A) 0,3
B) 0,5
C) 0,9
D) 1,8
E) 2,7
Clique aqui para ver a resolução.
QUESTÃO 147. Num certo momento de um jogo digital, a tela apresenta a imagem representada na figura. O ponto Q1 representa a posição de um jogador que está com a bola, os pontos Q2, Q3, Q4, Q5 e Q6 também indicam posições de jogadores da mesma equipe, e os pontos A e B indicam os dois pés da trave mais próxima deles. No momento da partida retratado, o jogador Q1 tem a posse da bola, que será passada para um dos outros jogadores das posições Qn, n ∈ {2, 3, 4, 5, 6}, cujo ângulo AQnB tenha a mesma medida do ângulo AQ1B.
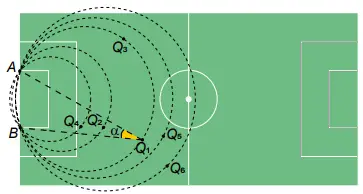
Qual é o jogador que receberá a bola?
A) Q2
B) Q3
C) Q4
D) Q5
E) Q6
Clique aqui para ver a resolução.
QUESTÃO 148. O triângulo da figura é denominado triângulo mágico. Nos círculos, escrevem-se os números de 1 a 6, sem repetição, com um número em cada círculo. O objetivo é distribuir os números de forma que as somas dos números em cada lado do triângulo sejam iguais.
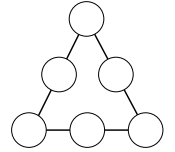
Considere que os números colocados nos vértices do triângulo estejam em progressão aritmética de razão igual a 2.
Nas condições propostas, quais as possíveis soluções para as somas dos números que formam os lados do triângulo?
A) Há somente uma solução possível, e as somas em cada lado do triângulo são iguais a 7.
B) Há somente uma solução possível, e as somas em cada lado do triângulo são iguais a 9.
C) Há somente duas soluções possíveis, uma em que as somas em cada lado do triângulo são iguais a 7 e outra em que as somas são iguais a 9.
D) Há somente duas soluções possíveis, uma em que as somas em cada lado do triângulo são iguais a 9 e outra em que as somas são iguais a 12.
E) Há somente duas soluções possíveis, uma em que as somas em cada lado do triângulo são iguais a 10 e outra em que as somas são iguais a 11.
Clique aqui para ver a resolução
QUESTÃO 149. No alojamento de uma universidade, há alguns quartos com o padrão superior ao dos demais. Um desses quartos ficou disponível, e muitos estudantes se candidataram para morar no local. Para escolher quem ficará com o quarto, um sorteio será realizado. Para esse sorteio, cartões individuais com os nomes de todos os estudantes inscritos serão depositados em uma urna, sendo que, para cada estudante de primeiro ano, será depositado um único cartão com seu nome; para cada estudante de segundo ano, dois cartões com seu nome; e, para cada estudante de terceiro ano, três cartões com seu nome. Foram inscritos 200 estudantes de primeiro ano, 150 de segundo ano e 100 de terceiro ano. Todos os cartões têm a mesma probabilidade de serem sorteados.
Qual a probabilidade de o vencedor do sorteio ser um estudante de terceiro ano?
A) 1/2
B) 1/3
C) 1/8
D) 2/9
E) 3/8
Clique aqui para ver a resolução
QUESTÃO 150. A água utilizada pelos 75 moradores de um vilarejo provém de um reservatório de formato cilíndrico circular reto cujo raio da base mede 5 metros, sempre abastecido no primeiro dia de cada mês por caminhões-pipa. Cada morador desse vilarejo consome, em média, 200 litros de água por dia. No mês de junho de um determinado ano, o vilarejo festejou o dia do seu padroeiro e houve um gasto extra de água nos primeiros 20 dias. Passado esse período, as pessoas verificaram a quantidade de água presente no reservatório e constataram que o nível da coluna de água estava em 1,5 metro. Decidiram, então, fazer um racionamento de água durante os 10 dias seguintes. Considere 3 como aproximação para π.
Qual é a quantidade mínima de água, em litro, que cada morador, em média, deverá economizar por dia, de modo que o reservatório não fique sem água nos próximos 10 dias?
A) 50
B) 60
C) 80
D) 140
E) 150
Clique aqui para ver a resolução
QUESTÃO 151. Em janeiro do ano passado, a direção de uma fábrica abriu uma creche para os filhos de seus funcionários, com 10 salas, cada uma com capacidade para atender 10 crianças a cada ano. As vagas são sorteadas entre os filhos dos funcionários inscritos, enquanto os não contemplados pelo sorteio formam uma lista de espera. No ano passado, a lista de espera teve 400 nomes e, neste ano, esse número cresceu 10%.
A direção da fábrica realizou uma pesquisa e constatou que a lista de espera para o próximo ano terá a mesma quantidade de nomes da lista de espera deste ano. Decidiu, então, construir, ao longo desse ano, novas salas para a creche, também com capacidade de atendimento para 10 crianças cada, de modo que o número de nomes na lista de espera no próximo ano seja 25% menor que o deste ano.
O número mínimo de salas que deverão ser construídas é
A) 10.
B) 11.
C) 13.
D) 30.
E) 33.
Clique aqui para ver a resolução
QUESTÃO 152. Os números figurados pentagonais provavelmente foram introduzidos pelos pitagóricos por volta do século V a.C. As figuras ilustram como obter os seis primeiros deles, sendo os demais obtidos seguindo o mesmo padrão geométrico.
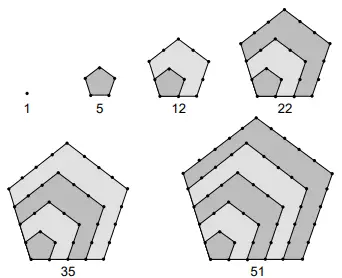
O oitavo número pentagonal é
A) 59.
B) 83.
C) 86.
D) 89.
E) 92.
Clique aqui para ver a resolução
QUESTÃO 153. A figura ilustra uma roda-gigante no exato instante em que a cadeira onde se encontra a pessoa P está no ponto mais alto dessa roda-gigante.
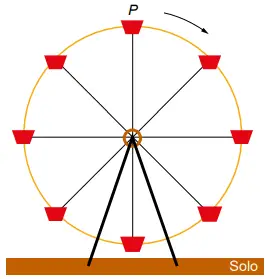
Com o passar do tempo, à medida que a roda-gigante gira, com velocidade angular constante e no sentido horário, a altura da cadeira onde se encontra a pessoa P, em relação ao solo, vai se alterando.
O gráfico que melhor representa a variação dessa altura, em função do tempo, contado a partir do instante em que a cadeira da pessoa P se encontra na posição mais alta da roda-gigante, é
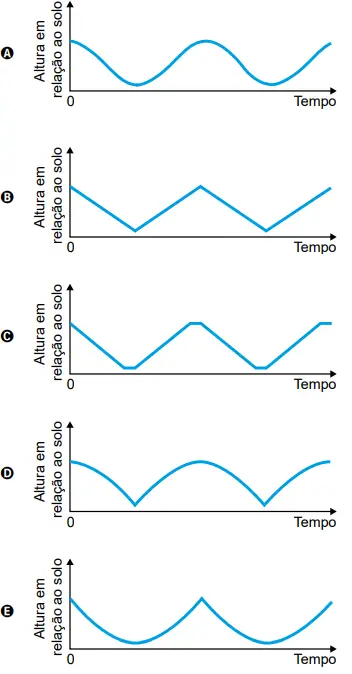
Clique aqui para ver a resolução.
QUESTÃO 154. Um professor, para promover a aprendizagem dos estudantes em estatística, propôs uma atividade. O objetivo era verificar o percentual de estudantes com massa corporal abaixo da média e altura acima da média de um grupo de estudantes. Para isso, usando uma balança e uma fita métrica, avaliou uma amostra de dez estudantes, anotando as medidas observadas. O gráfico apresenta a massa corporal, em quilograma, e a altura, em metro, obtidas na atividade.
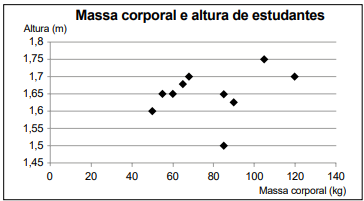
Após a coleta dos dados, os estudantes calcularam a média dos valores obtidos, referentes à massa corporal e à altura, obtendo, respectivamente, 80 kg e 1,65 m.
Qual é o percentual de estudantes dessa amostra com massa corporal abaixo da média e altura acima da média?
A) 10
B) 20
C) 30
D) 50
E) 70
Clique aqui para ver a resolução
QUESTÃO 155. Um pescador tem um custo fixo diário de R$ 900,00 com combustível, iscas, manutenção de seu barco e outras pequenas despesas. Ele vende cada quilograma de peixe por R$ 5,00. Sua meta é obter um lucro mínimo de R$ 800,00 por dia. Sozinho, ele consegue, ao final de um dia de trabalho, pescar 180 kg de peixe, o que é suficiente apenas para cobrir o custo fixo diário. Portanto, precisa contratar ajudantes, pagando para cada um R$ 250,00 por dia de trabalho. Além desse valor, 4% da receita obtida pela venda de peixe é repartida igualmente entre os ajudantes. Considerando o tamanho de seu barco, ele pode contratar até 5 ajudantes. Ele sabe que com um ajudante a pesca diária é de 300 kg e que, a partir do segundo ajudante contratado, aumenta-se em 100 kg a quantidade de peixe pescada por ajudante em um dia de trabalho.
A quantidade mínima de ajudantes que esse pescador precisa contratar para conseguir o lucro diário pretendido é
A) 1.
B) 2.
C) 3.
D) 4.
E) 5.
Clique aqui para ver a resolução
QUESTÃO 156. Um agricultor é informado sobre um método de proteção para sua lavoura que consiste em inserir larvas específicas, de rápida reprodução. A reprodução dessas larvas faz com que sua população multiplique-se por 10 a cada 3 dias e, para evitar eventuais desequilíbrios, é possível cessar essa reprodução aplicando-se um produto X. O agricultor decide iniciar esse método com 100 larvas e dispõe de 5 litros do produto X, cuja aplicação recomendada é de exatamente 1 litro para cada população de 200 000 larvas. A quantidade total do produto X de que ele dispõe deverá ser aplicada de uma única vez.
Quantos dias após iniciado esse método o agricultor deverá aplicar o produto X?
A) 2
B) 4
C) 6
D) 12
E) 18
Clique aqui para ver a resolução
QUESTÃO 157. Ao realizar o cadastro em um aplicativo de investimentos, foi solicitado ao usuário que criasse uma senha, sendo permitido o uso somente dos seguintes caracteres:
• algarismos de 0 a 9;
• 26 letras minúsculas do alfabeto;
• 26 letras maiúsculas do alfabeto;
• 6 caracteres especiais !, @, #, $, *, &.
Três tipos de estruturas para senha foram apresentadas ao usuário:
• tipo I: formada por quaisquer quatro caracteres distintos, escolhidos dentre os permitidos;
• tipo II: formada por cinco caracteres distintos, iniciando por três letras, seguidas por um algarismo e, ao final, um caractere especial;
• tipo III: formada por seis caracteres distintos, iniciando por duas letras, seguidas por dois algarismos e, ao final, dois caracteres especiais.
Considere p1, p2 e p3 as probabilidades de se descobrirem ao acaso, na primeira tentativa, as senhas dos tipos I, II e III, respectivamente.
Nessas condições, o tipo de senha que apresenta a menor probabilidade de ser descoberta ao acaso, na primeira tentativa, é o
A) tipo I, pois p1 < p2 < p3
B) tipo I, pois tem menor quantidade de caracteres.
C) tipo II, pois tem maior quantidade de letras.
D) tipo III, pois p3 < p2 < p1
E) tipo III, pois tem maior quantidade de caracteres.
Clique aqui para ver a resolução
Está gostando da resolução completa da prova de Matemática do ENEM 2023? Deixe o seu comentário.
QUESTÃO 158. Em um colégio público, a admissão no primeiro ano se dá por sorteio. Neste ano há 55 candidatos, cujas inscrições são numeradas de 01 a 55. O sorteio de cada número de inscrição será realizado em etapas, utilizando-se duas urnas. Da primeira urna será sorteada uma bola, dentre bolas numeradas de 0 a 9, que representará o algarismo das unidades do número de inscrição a ser sorteado e, em seguida, da segunda urna, será sorteada uma bola para representar o algarismo das dezenas desse número. Depois do primeiro sorteio, e antes de se sortear o algarismo das dezenas, as bolas que estarão presentes na segunda urna serão apenas aquelas cujos números formam, com o algarismo já sorteado, um número de 01 a 55.
As probabilidades de os candidatos de inscrição número 50 e 02 serem sorteados são, respectivamente,
a) 1/50 e 1/60
b) 1/50 e 1/50
c) 1/50 e 1/10
d) 1/55 e 1/54
d) 1/100 e 1/100
Clique aqui para ver a resolução
QUESTÃO 159. O esquema mostra como a intensidade luminosa decresce com o aumento da profundidade em um rio, sendo L0 a intensidade na sua superfície.
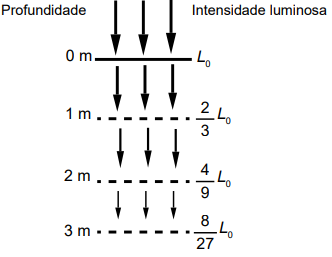
Considere que a intensidade luminosa diminui, a cada metro acrescido na profundidade, segundo o mesmo padrão do esquema.
A intensidade luminosa correspondente à profundidade de 6 m é igual a
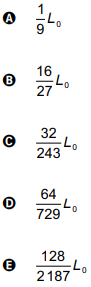
Clique aqui para ver a resolução
QUESTÃO 160. Analisando as vendas de uma empresa, o gerente concluiu que o montante diário arrecadado, em milhar de real, poderia ser calculado pela expressão
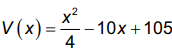
em que os valores de x representam os dias do mês, variando de 1 a 30.
Um dos fatores para avaliar o desempenho mensal da empresa é verificar qual é o menor montante diário V0 arrecadado ao longo do mês e classificar o desempenho conforme as categorias apresentadas a seguir, em que as quantidades estão expressas em milhar de real.
• Ótimo: V0 ≥ 24
• Bom: 20 ≤ V0 < 24
• Normal: 10 ≤ V0 < 20
• Ruim: 4 ≤ V0 < 10
• Péssimo: V0 < 4
No caso analisado, qual seria a classificação do desempenho da empresa?
A) Ótimo.
B) Bom.
C) Normal.
D) Ruim.
E) Péssimo.
Clique aqui para ver a resolução
QUESTÃO 161. Dirigir após ingerir bebidas alcoólicas é uma atitude extremamente perigosa, uma vez que, a partir da primeira dose, a pessoa já começa a ter perda de sensibilidade de movimentos e de reflexos. Apesar de a eliminação e absorção do álcool depender de cada pessoa e de como o organismo consegue metabolizar a substância, ao final da primeira hora após a ingestão, a concentração de álcool (C) no sangue corresponde a aproximadamente 90% da quantidade (q) de álcool ingerida, e a eliminação total dessa concentração pode demorar até 12 horas.
Nessas condições, ao final da primeira hora após a ingestão da quantidade q de álcool, a concentração C dessa substância no sangue é expressa algebricamente por
A) C = 0,9q
B) C = 0,1q
C) C = 1 − 0,1q
D) C = 1 − 0,9q
E) C = q − 10
Clique aqui para ver a resolução
QUESTÃO 162. Um investidor iniciante observou o gráfico que apresenta a evolução dos valores de duas criptomoedas A e B em relação ao tempo.
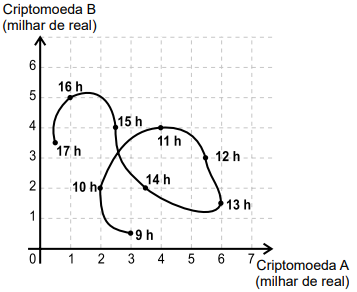
Durante horas consecutivas, esses valores foram observados em nove instantes, representados por horas exatas.
Em quantos desses instantes a criptomoeda A estava mais valorizada do que a criptomoeda B?
A) 3
B) 4
C) 6
D) 7
E) 9
Clique aqui para ver a resolução
QUESTÃO 163. A exposição a alguns níveis sonoros pode causar lesões auditivas. Por isso, em uma indústria, são adotadas medidas preventivas de acordo com a máquina que o funcionário opera e o nível N de intensidade do som, medido em decibel (dB), a que o operário é exposto,
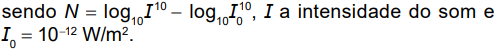
Quando o som é considerado baixo, ou seja, N = 48 dB ou menos, deve ser utilizada a medida preventiva I. No caso de o som ser moderado, quando N está no intervalo (48 dB, 55 dB), deve ser utilizada a medida preventiva II. Quando o som é moderado alto, que equivale a N no intervalo (55 dB, 80 dB), a medida preventiva a ser usada é a III. Se N estiver no intervalo (80 dB, 115 dB), quando o som é considerado alto, deve ser utilizada a medida preventiva IV. E se o som é considerado muito alto, com N maior que 115 dB, deve-se utilizar a medida preventiva V.
Uma nova máquina, com I = 8 × 10−8 W/m2, foi adquirida e será classificada de acordo com o nível de ruído que produz.
Considere 0,3 como aproximação para log102.
O funcionário que operará a nova máquina deverá adotar a medida preventiva
A) I.
B) II.
C) III.
D) IV.
E) V.
Clique aqui para ver a resolução
QUESTÃO 164. Um artista plástico esculpe uma escultura a partir de um bloco de madeira de lei, em etapas. Inicialmente, esculpe um cone reto com 36 cm de altura e diâmetro da base medindo 18 cm. Em seguida, remove desse cone um cone menor, cujo diâmetro da base mede 6 cm, obtendo, assim, um tronco de cone, conforme ilustrado na figura.
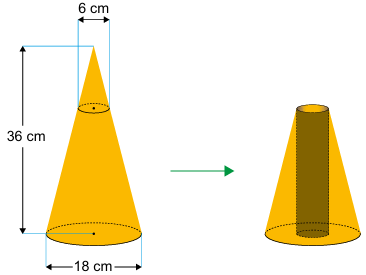
Em seguida, perfura esse tronco de cone, removendo um cilindro reto, de diâmetro 6 cm, cujo eixo de simetria é o mesmo do cone original. Dessa forma, ao final, a escultura tem a forma de um tronco de cone com uma perfuração cilíndrica de base a base.
O tipo de madeira utilizada para produzir essa escultura tem massa igual a 0,6 g por centímetro cúbico de volume. Utilize 3 como aproximação para π.
Qual é a massa, em grama, dessa escultura?
A) 1 198,8
B) 1 296,0
C) 1 360,8
D) 4 665,6
E) 4 860,0
Clique aqui para ver a resolução
QUESTÃO 165. Os 100 funcionários de uma empresa estão distribuídos em dois setores: Produção e Administração. Os funcionários de um mesmo setor recebem salários com valores iguais. O quadro apresenta a quantidade de funcionários por setor e seus respectivos salários.
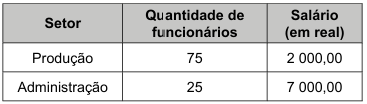
A média dos salários dos 100 funcionários dessa empresa, em real, é
A) 2 000,00.
B) 2 500,00.
C) 3 250,00.
D) 4 500,00.
E) 9 000,00.
Clique aqui para ver a resolução
QUESTÃO 166. Visando atrair mais clientes, o gerente de uma loja anunciou uma promoção em que cada cliente que realizar uma compra pode ganhar um voucher para ser usado em sua próxima compra. Para ganhar seu voucher, o cliente precisa retirar, ao acaso, uma bolinha de dentro de cada uma das duas urnas A e B disponibilizadas pelo gerente, nas quais há apenas bolinhas pretas e brancas. Atualmente, a probabilidade de se escolher, ao acaso, uma bolinha preta na urna A é igual a 20% e a probabilidade de se escolher uma bolinha preta na urna B é 25%. Ganha o voucher o cliente que retirar duas bolinhas pretas, uma de cada urna.
Com o passar dos dias, o gerente percebeu que, para a promoção ser viável aos negócios, era preciso alterar a probabilidade de acerto do cliente sem alterar a regra da promoção. Para isso, resolveu alterar a quantidade de bolinhas brancas na urna B de forma que a probabilidade de um cliente ganhar o voucher passasse a ser menor ou igual a 1%. Sabe-se que a urna B tem 4 bolinhas pretas e que, em ambas as urnas, todas as bolinhas têm a mesma probabilidade de serem retiradas.
Qual é o número mínimo de bolinhas brancas que o gerente deve adicionar à urna B?
A) 20
B) 60
C) 64
D) 68
E) 80
Clique aqui para ver a resolução
QUESTÃO 167. Estudantes trabalhando com robótica criaram uma “torneira inteligente” que automatiza sua abertura e seu fechamento durante a limpeza das mãos. A tecnologia funciona da seguinte forma: ao se colocarem as mãos sob a torneira, ela libera água durante 3 segundos para que a pessoa possa molhá-las. Em seguida, interrompe o fornecimento de água por 5 segundos, enquanto a pessoa ensaboa suas mãos, e finaliza o ciclo liberando água para o enxágue por mais 3 segundos. Considere o tempo ( t ), em segundo, contado a partir do instante em que se inicia o ciclo. A vazão de água nessa torneira é constante.
Um esboço de gráfico que descreve o volume de água acumulado, em litro, liberado por essa torneira durante um ciclo de lavagem das mãos, em função do tempo ( t ), em segundo, é
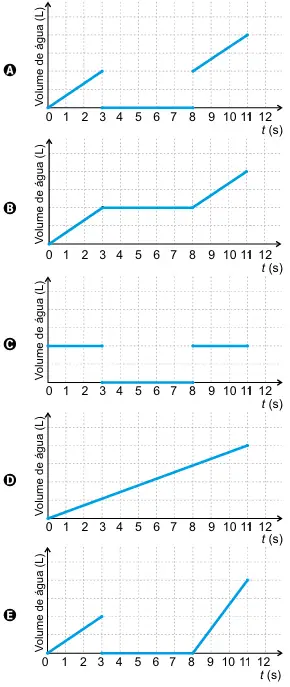
Clique aqui para ver a resolução
QUESTÃO 168. As características culturais variam de povo para povo. Há notícias de um povo que possuía formas de contar diferentes das nossas, como indicado no quadrinho a seguir.
Segundo o padrão de contagem indicado na figura, as representações dos numerais cinco e sete, nessa cultura, devem ser, respectivamente,
A) okosa urapum urapum urapum e okosa okosa urapum urapum urapum.
B) okosa okosa urapum e okosa okosa okosa okosa urapum.
C) okosa okosa urapum e okosa okosa okosa urapum.
D) okosa urapum urapum e okosa urapum okosa urapum urapum.
E) okosa okosa urapum e okosa okosa okosa okosa.
Clique aqui para ver a resolução
QUESTÃO 169. Um tipo de semente necessita de bastante água nos dois primeiros meses após o plantio. Um produtor pretende estabelecer o melhor momento para o plantio desse tipo de semente, nos meses de outubro a março. Após consultar a previsão do índice mensal de precipitação de chuva (ImPC) da região onde ocorrerá o plantio, para o período chuvoso de 2020 – 2021, ele obteve os seguintes dados:
• outubro/2020: ImPC = 250 mm;
• novembro/2020: ImPC = 150 mm;
• dezembro/2020: ImPC = 200 mm;
• janeiro/2021: ImPC = 450 mm;
• fevereiro/2021: ImPC = 100 mm;
• março/2021: ImPC = 200 mm.
Com base nessas previsões, ele precisa escolher dois meses consecutivos em que a média mensal de precipitação seja a maior possível.
No início de qual desses meses o produtor deverá plantar esse tipo de semente?
A) Outubro.
B) Novembro.
C) Dezembro.
D) Janeiro.
E) Fevereiro.
Clique aqui para ver a resolução
QUESTÃO 170. Uma loja vende seus produtos de duas formas: à vista ou financiado em três parcelas mensais iguais. Para definir o valor dessas parcelas nas vendas financiadas, a loja aumenta em 20% o valor do produto à vista e divide esse novo valor por 3. A primeira parcela deve ser paga no ato da compra, e as duas últimas, em 30 e 60 dias após a compra.
Um cliente da loja decidiu comprar, de forma financiada, um produto cujo valor à vista é R$ 1 500,00.
Utilize 5,29 como aproximação para √28.
A taxa mensal de juros compostos praticada nesse financiamento é de
A) 6,7%
B) 10%
C) 20%
D) 21,5%
E) 23,3%
Clique aqui para ver a resolução
QUESTÃO 171. Para concretar a laje de sua residência, uma pessoa contratou uma construtora. Tal empresa informa que o preço y do concreto bombeado é composto de duas partes: uma fixa, chamada de taxa de bombeamento, e uma variável, que depende do volume x de concreto utilizado. Sabe-se que a taxa de bombeamento custa R$ 500,00 e que o metro cúbico do concreto bombeado é de R$ 250,00.
A expressão que representa o preço y em função do volume x, em metro cúbico, é
A) y = 250x
B) y = 500x
C) y = 750x
D) y = 250x + 500
E) y = 500x + 250
Clique aqui para ver a resolução
QUESTÃO 172. Uma empresa de segurança domiciliar oferece o serviço de patrulha noturna, no qual vigilantes em motocicletas fazem o monitoramento periódico de residências. A empresa conta com uma base, de onde acompanha o trajeto realizado pelos vigilantes durante as patrulhas e orienta o deslocamento de equipes de reforço quando necessário. Numa patrulha rotineira, sem ocorrências, um vigilante conduziu sua motocicleta a uma velocidade constante durante todo o itinerário estabelecido, levando 30 minutos para conclusão. De acordo com os registros do GPS alocado na motocicleta, a distância da posição do vigilante à base, ao longo do tempo de realização do trajeto, é descrita pelo gráfico.

A vista superior da trajetória realizada pelo vigilante durante a patrulha registrada no gráfico é descrita pela representação

Clique aqui para ver a resolução
QUESTÃO 173. Um supermercado conta com cinco caixas disponíveis para pagamento. Foram instaladas telas que apresentam o tempo médio gasto por cada caixa para iniciar e finalizar o atendimento de cada cliente, e o número de pessoas presentes na fila de cada caixa em tempo real. Um cliente, na hora de passar sua compra, sabendo que cada um dos cinco caixas iniciará um novo atendimento naquele momento, pretende gastar o menor tempo possível de espera na fila. Ele observa que as telas apresentavam as informações a seguir.
• Caixa I: atendimento 12 minutos, 5 pessoas na fila.
• Caixa II: atendimento 6 minutos, 9 pessoas na fila.
• Caixa III: atendimento 5 minutos, 6 pessoas na fila.
• Caixa IV: atendimento 15 minutos, 2 pessoas na fila.
• Caixa V: atendimento 9 minutos, 3 pessoas na fila.
Para alcançar seu objetivo, o cliente deverá escolher o caixa
A) I.
B) II.
C) III.
D) IV.
E) V.
Clique aqui para ver a resolução
QUESTÃO 174. As figuras pintadas no quadro da sala de estar de uma residência representam as silhuetas de parte das torres de um castelo e, ao fundo, a de uma lua cheia. A lua foi pintada na forma de um círculo, e o telhado da torre mais alta, na forma de triângulo equilátero, foi pintado sobrepondo parte da lua. O centro da lua coincide com um dos vértices do telhado da torre mais alta.
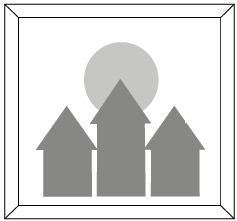
Nesse quadro, a parte da lua escondida atrás da torre mais alta do castelo pode ser representada por um
A) cone.
B) setor circular.
C) segmento circular.
D) triângulo isósceles.
E) arco de circunferência.
Clique aqui para ver a resolução
QUESTÃO 175. Na planta baixa de um clube, a piscina é representada por um quadrado cuja área real mede 400 m². Ao redor dessa piscina, será construída uma calçada, de largura constante igual a 5 m.
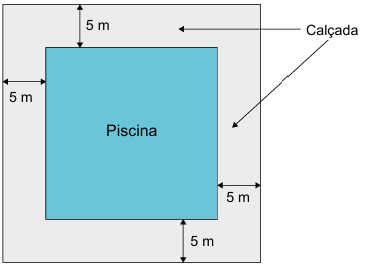
Qual é a medida da área, em metro quadrado, ocupada pela calçada?
A) 1 000
B) 900
C) 600
D) 500
E) 400
Clique aqui para ver a resolução
QUESTÃO 176. Uma pessoa caminha por 30 minutos e utiliza um aplicativo instalado em seu celular para monitorar a variação da intensidade do sinal de internet recebido pelo aparelho durante o deslocamento. Chegando ao seu destino, o aplicativo forneceu este gráfico:
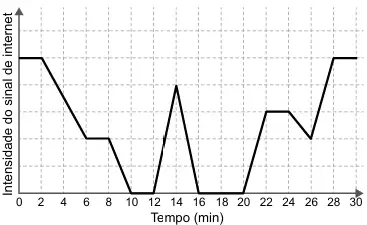
Por quantos minutos, durante essa caminhada, o celular dessa pessoa ficou sem receber sinal de internet?
A) 6
B) 8
C) 10
D) 14
E) 24
Clique aqui para ver a resolução
QUESTÃO 177 – ANULADA
QUESTÃO 178. A figura representa uma escada com três degraus, construída em concreto maciço, com suas medidas especificadas.
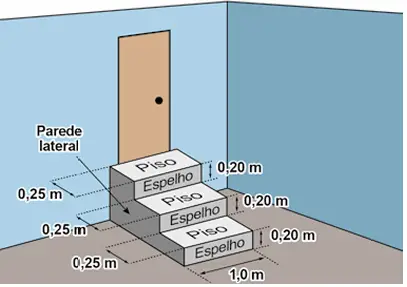
Nessa escada, pisos e espelhos têm formato retangular, e as paredes laterais têm formato de um polígono cujos lados adjacentes são perpendiculares. Pisos, espelhos e paredes laterais serão revestidos em cerâmica.
A área a ser revestida em cerâmica, em metro quadrado, mede
A) 1,20.
B) 1,35.
C) 1,65.
D) 1,80.
E) 1,95.
Clique aqui para ver a resolução
QUESTÃO 179. Uma pessoa comprou um ingresso para o cinema em cuja entrada está afixado um mapa com a representação bidimensional do posicionamento das poltronas, conforme a figura. Essa pessoa, após consultar o mapa, começou a subir uma das escadas e parou na posição indicada pela estrela, direcionada para o norte. Ela conferiu seu bilhete e observou que, para encontrar sua poltrona, deveria partir do ponto onde estava, continuar subindo a escada na direção norte por mais quatro fileiras e olhar à sua direita, e sua poltrona será a terceira.
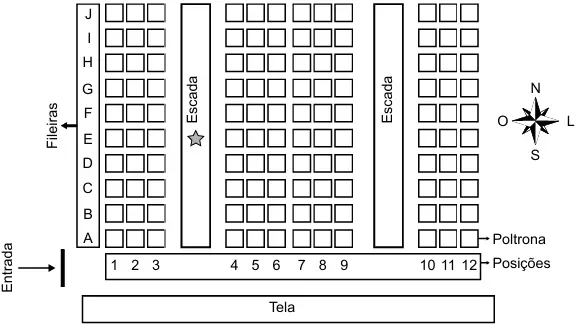
Nesse cinema, as poltronas são identificadas por uma letra, que indica a fileira, e um número, que fornece a posição da poltrona na fileira, respectivamente.
A poltrona dessa pessoa é a identificada por
A) A6.
B) H1.
C) H6.
D) I1.
E) I6.
Clique aqui para ver a resolução
QUESTÃO 180. O metrô de um município oferece dois tipos de tíquetes com colorações diferentes, azul e vermelha, sendo vendidos em cartelas, cada qual com nove tíquetes da mesma cor e mesmo valor unitário. Duas cartelas de tíquetes azuis e uma cartela de tíquetes vermelhos são vendidas por R$ 32,40. Sabe-se que o preço de um tíquete azul menos o preço de um tíquete vermelho é igual ao preço de um tíquete vermelho mais cinco centavos.
Qual o preço, em real, de uma cartela de tíquetes vermelhos?
A) 4,68
B) 6,30
C) 9,30
D) 10,50
E) 10,65
Clique aqui para ver a resolução
Gostou da resolução completa da prova de Matemática do ENEM 2023? Deixe o seu comentário.
