QUESTÃO 137. O mastro de uma bandeira foi instalado perpendicularmente ao solo em uma região plana. Devido aos fortes ventos, três cabos de aço, de mesmo comprimento, serão instalados para dar sustentação ao mastro. Cada cabo de aço ficará perfeitamente esticado, com uma extremidade num ponto P do mastro, a uma altura h do solo, e a outra extremidade, num ponto no chão, como mostra a figura.
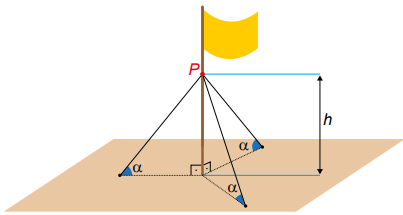
Os cabos de aço formam um ângulo α com o plano do chão.
Por medida de segurança, há apenas três opções de instalação:
- opção I: h = 11 m e α = 30°
- opção II: h = 12 m e α = 45°
- opção III: h = 18 m e α = 60°
A opção a ser escolhida é aquela em que a medida dos cabos seja a menor possível.
Qual será a medida, em metro, de cada um dos cabos a serem instalados?
a) 22√3 / 3
b) 11√2
c) 12√2
d) 12√3
e) 22
Resolução
Observe que o mastro os cabos e o chão formam triângulos retângulos.
Sabemos o ângulo α, o cateto oposto (h) e a hipotenusa (comprimento do cabo, que chamaremos de x).
Calcularemos o valor de x em cada um dos casos, considerando que em um triângulo retângulo, o seno é igual a divisão do cateto oposto pela hipotenusa.
Opção I
senα = h/x
sen30º = 11/x
1/2 = 11/x
x = 22
Opção II
senα = h/x
sen45º = 12/x
√2/2 = 12/x
√2x = 2.12
√2x = 24
x = 24/√2
x = (24.√2)/(√2.√2)
x = 24.√2/2
x = 12√2
Opção III
senα = h/x
sen60º = 18/x
√3/2 = 18/x
√3x = 2.18
√3x = 36
x = 36/√3
x = (36.√3)/(√3.√3)
x = 36.√3/3
x = 12√3
A opção II é a que o cabo possui o menor comprimento.
Resposta: C
