Confira um resumo sobre os principais conjuntos numéricos (naturais, inteiros, racionais, irracionais e reais).
O assunto é base para muitos conteúdos e cai com frequência em vários concursos, principalmente os de nível médio, além de ser muito cobrado no ENEM.
Bons estudos!
1. Introdução:
Podemos chamar de conjuntos numéricos certos agrupamentos de algarismos que possuem alguma característica em comum.
2. Conjuntos dos números naturais.
Conjunto representado pela letra N maiúscula, englobando todos os números inteiros positivos e o zero. Veja:
N = {0, 1, 2, 3, 4, 5, 6, …}
Clique aqui para saber mais sobre os números naturais.
3. Conjunto dos números inteiros.
Conjunto representado pela letra Z maiúscula, englobando todos os números inteiros positivos, negativos e o zero.
Veja:
Z = {…, -2, -1, 0, 1, 2,…}
Clique aqui para saber mais sobre os números inteiros.
4. Conjunto dos números racionais.
Conjunto representado pela letra Q maiúscula, englobando todos os números inteiros positivos, negativos, o zero, números na forma decimal e os números fracionários.
Obs: Chamamos de dízimas periódicas os resultados de uma divisão onde temos repetição de algarismos após a vírgula. Exemplo: 0,45454545…. Toda dízima periódica pode ser representada por fração. Veja:
0,222222… = 2/9
0,343434… = 34/99
Clique aqui para saber mais sobre os números racionais.
Clique aqui para saber mais sobre as dízimas periódicas.
5. Conjunto dos números irracionais.
Conjunto representado pela letra I maiúscula, englobando os números que não possuem representação fracionária. São considerados dízimas não periódicas, ou seja, não possuem um padrão após a vírgula. Veja:
1,23534366332…
3,62465842359…
Clique aqui para saber mais sobre os números irracionais.
6. Relação entre os conjuntos numéricos
Diante do que estudamos até agora, podemos construir a seguinte figura:
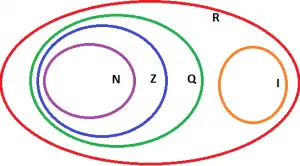
Observe que:
– Todos os elementos do conjunto N também são elementos do conjunto Z;
– Todos os elementos do conjunto Z também são elementos do conjunto Q;
– Um elemento do conjunto I não pode pertencer de forma alguma do conjunto Q;
– Todos os elementos dos conjuntos Q e I também são elementos do conjunto maior R;
7. Simbologia.
A={ } ou A=Ø O conjunto A é vazio, ou seja, não possui elementos
5 Є N O elemento 5 pertence ao conjunto N
A⊂B Todos os elementos do conjunto A também pertencem ao conjunto B
B⊃A O conjunto B contém todos os elementos do conjunto A
∃x Є A Existe elemento x pertencente ao conjunto A
A∪B União dos conjuntos A e B. Exemplo: {4, 5} ∪ {4, 7, 8} = {4, 5, 7, 8}
A∩B Intersecção dos conjuntos A e B. Exemplo: {4, 5} ∩ {4, 7, 8} = {4}
A-B Conjunto formado pelos elementos que pertencem a A e não pertencem a B
∌ Não pertence
⊄ Não contém
⊅ Não está contido
∄ Não existe
Veja no YouTube:
Gostou da nossa publicação sobre os conjuntos numéricos?
Deixe o seu comentário.
