Vamos aprender a identificar os números inteiros, suas propriedades e aplicações?
Bom estudo!
Introdução
Agora que já aprendemos sobre o conjunto dos números naturais, estamos preparados para dar o próximo passo. Entender o que é o conjunto dos números inteiros.
Esse conjunto surgiu com a evolução da civilização, que passou a ter a necessidade de representar perdas e dívidas, ou seja, daí surgiram os números negativos.
Veja como é representado o conjunto dos números inteiros:
Z = {…, -4, -3, -2, -1, 0, 1, 2, 3, 4, …}
Repare que esse conjunto é representado pela letra Z e possui uma infinidade de elementos, tanto a esquerda quanto a direita do elemento zero.
Também é possível observar que o conjunto dos números inteiros abrange todos os números naturais mais os números negativos. Dizemos neste caso que N está contigo em Z, ou Z contém N.
Veja a representação geométrica de Z:
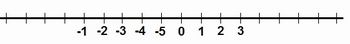
Subconjuntos de Z
Dentre os infinitos elementos de Z, existem alguns com características comuns, que podemos separar em outros conjuntos, também chamados de subconjuntos de Z. Veja:
- Conjunto dos números inteiros não nulos
Esse conjunto abrange os números inteiros sem o zero:
Z* = {…, -4, -3, -2, -1, 1, 2, 3, 4, …}
- Conjunto dos números inteiros não negativos
Esse conjunto exclui os números negativos. Nota-se que Z+ = N.
Z+ = { 0, 1, 2, 3, 4, …}
- Conjunto dos números inteiros positivos
Esse conjunto exclui os números negativos e o elemento zero.
Z*+ = {1, 2, 3, 4, …}
- Conjunto dos números inteiros não positivos
Esse conjunto exclui os números positivos.
Z_ = {…, -4, -3, -2, -1, 0}
- Conjunto dos números inteiros negativos
Esse conjunto exclui os números positivos e o elemento zero.
Z*_ = {…, -4, -3, -2, -1}
Algumas definições importantes:
- Números opostos: Dizemos que dois números são opostos um do outro quando a soma dos dois é igual a zero, ou, geometricamente, quando a distância em relação à origem é a mesma. Ex: -4 e 4.
- Módulo de um número inteiro: Chamamos de módulo, ou valor absoluto, de um número “a”, a distância da origem ao ponto que representa “a”. Para facilitar, basta excluir o sinal negativo do número. Ex: O módulo de -2 é 2. A representação dá-se da seguinte forma: |-2| = 2.
Gostou da nossa publicação sobre os números inteiros?
Deixe o seu comentário.
