Confira aqui a prova resolvida do concurso para a Polícia Militar do Estado do Amazonas (PM AM – 2022). O concurso foi organizado pela FGV, com edital em 2021 e prova aplicada em 2022.
31. Uma fila para vacinação se formou no posto de saúde e nela estão Sílvio e Mário. A fila tem 42 pessoas, Sílvio está na frente de Mario e há 4 pessoas entre eles. Sabe-se que o número de pessoas que estão atrás de Mário é o dobro do número de pessoas que estão à frente de Sílvio. O lugar que Mário ocupa na fila é o:
(A) 13º.
(B) 16º.
(C) 17º.
(D) 18º.
(E) 19º.
Resolução
Observe que existe uma fila com 42 pessoas, Sílvio está à frente de Mário, existindo 4 pessoas entre os dois. Temos ainda que o número de pessoas atrás de Mário é o dobro do número de pessoas à frente de Silvio.
Considerando que x representa a quantidade de pessoas à frente de Silvio, temos:
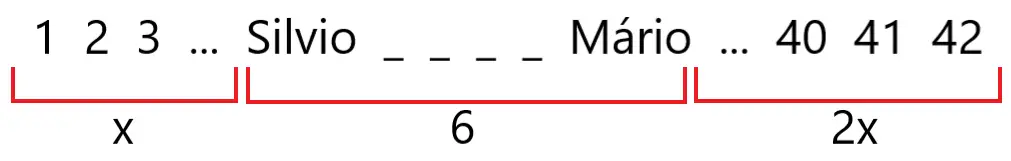
Observando a imagem acima, temos que:
x + 6 + 2x = 42
3x = 42 – 6
3x = 36
x = 36/3
x = 12
Sabendo que x = 12, podemos concluir que Mário ocupa a posição:
12 + 6 = 18
Resposta: D
32. Em certo estado, a Coordenadoria de Missões Especiais tem seu diretor trocado de 8 em 8 meses e a Coordenadoria de Operações tem seu diretor trocado de 10 em 10 meses. Sabe-se que em julho de 2021 as duas coordenadorias tiveram seus diretores trocados simultaneamente. A próxima troca simultânea dos dois diretores ocorrerá em
(A) Outubro de 2023.
(B) Março de 2024.
(C) Julho de 2024.
(D) Novembro de 2024.
(E) Janeiro de 2025.
Resolução
A Missões Especiais troca o diretor a cada 8 meses, enquanto a Operações troca a cada 10 meses.
Precisamos calcular quando será a próxima troca simultânea, ou seja, o mmc de 8 e 10.
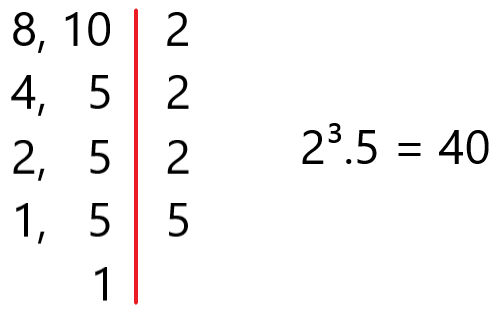
Considerando que mmc(8,10) = 40, podemos concluir que a troca simultânea ocorre a cada 40 meses, ou seja, 40 meses a partir de julho de 2021.
07/2021 + 40 meses = 11/2024
Resposta: D
33. Em uma fila com 12 cadeiras, três delas foram ocupadas aleatoriamente. A cadeira em que Valter deverá se sentar será sorteada entre as cadeiras que estão vazias. A probabilidade de que Valter não se sente ao lado de nenhuma pessoa já sentada é, no mínimo:
(A) 1/2.
(B) 1/3.
(C) 2/3.
(D) 1/4.
(E) 1/6.
Resolução
A questão quer saber a probabilidade mínima de Valter não sentar ao lado de nenhuma pessoa já sentada.
Vamos considerar o pior cenário possível, ou seja, aquele que Valter tem menos opções.
Observe na figura abaixo que este cenário é o que possui pessoas sentadas (em azul) nas posições 2,5 e 8.
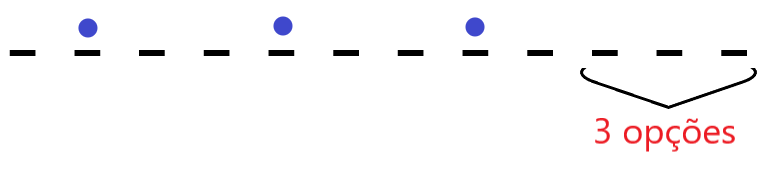
Valter possui 3 opções em 9 cadeiras disponíveis.
3/9 = 1/3
Resposta: B
34. Considere a afirmação: “Nenhum soldado escuta mal”. A sua negação é:
(A) Há pelo menos um soldado que escuta mal.
(B) Vários soldados escutam mal.
(C) Todos os soldados escutam mal.
(D) Todos os soldados escutam bem.
(E) Todas as pessoas que escutam bem são soldados.
Resolução
A negação de “nenhum” é “pelo menos um”, ou seja, a negação de “Nenhum soldado escuta mal” é “Há pelo menos um soldado que escuta mal”.
Resposta: A
35. Segundo dados da PM do Estado do Amazonas, o número de veículos recuperados em 2018 foi 320 e o número de veículos recuperados em 2020 foi 870. Comparando os dados desses dois anos, o número de veículos recuperados em 2020 foi maior que o de 2018 em cerca de:
(A) 130%.
(B) 140%.
(C) 150%.
(D) 160%.
(E) 170%.
Resolução
O número de veículos apreendidos passou de 320 em 2018 para 870 em 2020, ou seja, podemos calcular a resposta através da divisão 870/320.
Como 870/320 = 2,71, podemos concluir que o aumento foi de aproximadamente 170%.
Resposta: E
36. Sabe-se que a sentença “Se o sapato é preto, então a meia é preta ou o cinto é preto” é FALSA. É correto concluir que
(A) o sapato é preto, a meia não é preta, o cinto não é preto.
(B) o sapato é preto, a meia é preta, o cinto não é preto.
(C) o sapato é preto, a meia é preta, o cinto é preto.
(D) o sapato não é preto, a meia não é preta, o cinto não é preto.
(E) o sapato não é preto, a meia é preta, o cinto é preto.
Resolução
Observe que temos uma proposição composta com uma implicação e uma disjunção:
A⇒(BvC)
Onde:
A: O sapato é preto
B: A meia é preta
C: O cinto é preto
Observando a tabela verdade de uma implicação, ela será falsa apenas quando A = V e (BvC) = F.
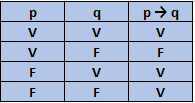
Já sabemos que A é V, ou seja, o sapato é preto.
Devemos analisar a tabela verdade da disjunção para verificarmos o(s) casos em que (BvC) = F.
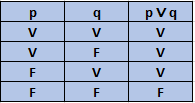
Observe que uma disjunção é F apenas quando ambas as proposições são F, ou seja, B é F e C é F.
Conclusão:
O sapato é preto, a meia não é preta e o cinto não é preto.
Resposta: A
37. O soldado Golias mediu o comprimento de sua cama em palmos e encontrou 8 palmos e meio. Um palmo de Golias mede 26 cm. O comprimento da cama de Golias é aproximadamente
(A) 2 metros.
(B) 2 metros e 10 centímetros.
(C) 2 metros e 20 centímetros.
(D) 2 metros e 30 centímetros.
(E) 2 metros e 40 centímetros.
Resolução
Devemos efetuar o produto:
8,5 palmos X 26 cm = 221 cm = 2,21 metros
Resposta: C
38. Rubinho pagou com juros uma conta já vencida. O valor total pago por Rubinho foi de R$ 483,00. Sabendo que Rubinho pagou 15% de juros sobre o valor inicial da conta, o valor dos juros foi de
(A) R$ 75,15.
(B) R$ 72,45.
(C) R$ 68,00.
(D) R$ 63,00.
(E) R$ 61,25.
Resolução
Observe que o valor inicial passou para R$ 483,00 após após um acréscimo de 15%
Podemos calcular o valor inicial através da divisão 483/1,15, onde 1,15 representa o acréscimo de 15% na forma decimal.
483/1,15 = 420
Calculando o valor dos juros:
483 – 420 = R$ 63
Resposta: D
39. O soldado Garcia vai liderar uma equipe de 3 soldados (ele incluído) para uma missão. Os outros 2 soldados da equipe serão sorteados aleatoriamente de um grupo de 6 soldados, sendo que um dos 6 é o soldado Ryan, amigo do soldado Garcia. A probabilidade de o soldado Ryan ser um dos 2 sorteados é
(A) 1/6.
(B) 1/5.
(C) 1/4.
(D) 1/3.
(E) 1/2
Resolução
Calcularemos inicialmente a quantidade total de opções, considerando que 2 soldados serão sorteados em um grupo de 6.
C(6,2) = 6!/2!(6-2)! = 6!/2!4! = 6.5.4!/2.4! = 30/2 = 15
Agora que sabemos a quantidade total, consideraremos que Ryan foi um dos sorteados e que o segundo soldado será sorteado em um grupo de 5, ou seja, 5 opções.
Probabilidade so soldado Ryan ser um dos 2 sorteados:
5/15 = 1/3
Resposta: D
40. Em um grupo de 45 soldados, 27 gostam de marchar e 38 gostam de praticar tiro ao alvo. Sejam: X: o número de soldados desse grupo que gostam de marchar e também de praticar tiro ao alvo; Y: o número de soldados desse grupo que não gostam nem de marchar nem de praticar tiro ao alvo. Nesse caso, é correto afirmar que
(A) X é no máximo 20.
(B) Y é no mínimo 7.
(C) quando X = 23, tem-se Y = 7.
(D) quando Y = 7, tem-se X = 20.
(E) quando Y = 5, tem-se X = 25. .
Resolução
As informações apresentadas pela questão estão no diagrama abaixo:
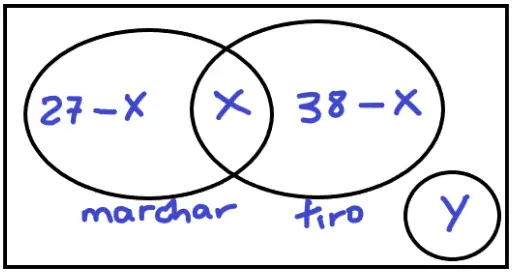
Como o grupo possui 45 soldados e se considerarmos que Y = 5, temos que:
27 – X + X + 38 – X + Y = 45
27 + 38 – X + 5 = 45
70 – X = 45
X = 70 – 45
X = 25
Resposta: E
Veja a resolução no YouTube:
Gostou da prova resolvida do concurso para a Polícia Militar do Estado do Amazonas, realizado em 2022 pela FGV?
Deixe o seu comentário.
