Confira aqui a prova resolvida (gabarito extraoficial) do concurso para a Polícia Militar do Estado de São Paulo (PM SP), realizado em 2018 pela Vunesp.
Lembrando que trata-se do segundo concurso Vunesp x PM SP de 2018.
Boa sorte!
Questão 19. Em uma gaveta há 24 canetas, sendo 1/6 delas verdes, 3/8 vermelhas, e as demais azuis. O número de canetas azuis que há nessa gaveta é
(A) 11.
(B) 9.
(C) 7.
(D) 10.
(E) 8.
Resolução
Sabendo que existem 24 canetas, calcularemos o total de canetas verdes e vermelhas:
24 . 1/6 = 4 canetas verdes
24 . 3/8 = 9 canetas vermelhas
Total de canetas azuis:
24 – 4 – 9 = 11
Resposta: A

Questão 20. Uma pessoa toma 3 medicamentos diferentes: A, B e C. O medicamento A ela toma a cada 4 horas, o medicamento B, a cada 6 horas, e o medicamento C, a cada 12 horas. Sabendo que às 9 horas do dia 1o de agosto essa pessoa tomou os 3 medicamentos juntos, o próximo dia e horário em que essa pessoa tomará esses 3 medicamentos juntos novamente será em
(A) 1 de agosto, às 12 horas.
(B) 2 de agosto, às 12 horas.
(C) 1 de agosto, às 24 horas.
(D) 2 de agosto, às 09 horas.
(E) 1 de agosto, às 21 horas.
Resolução
A pessoa toma 3 medicamentos diferentes, em intervalos de 4, 6 e 12 horas.
Como precisamos saber quando os medicamentos serão tomados juntos, basta calcular o mmc de 4, 6 e 12.
Como 12 é múltiplo de 4 e 6, temos que mmc(4, 6, 12) = 12.
Conclusão: Os três medicamentos são tomados juntos a cada 12 horas.
Como a pessoa tomou os três medicamentos ao mesmo tempo às 9 horas do dia 1º de agosto, ela voltará a tomar os três ao mesmo tempo 12 horas depois, ou seja, às 21 horas do mesmo dia.
Resposta: E
Questão 21. Em certo dia, em uma empresa onde trabalham 36 pessoas, a razão do número de pessoas resfriadas para o número de pessoas não resfriadas era 2/7. No dia seguinte, constatou-se que mais uma dessas pessoas estava resfriada. Assim, a razão do número de pessoas resfriadas para o número de pessoas não resfriadas passou a ser
a) 4/7
b) 1/2
c) 3/7
d) 1/3
e) 1/4
Resolução
Sabendo que a razão entre o número de pessoas resfriadas e o número de pessoas não resfriadas é 2/7, temos que a cada 9 pessoas que trabalharam no primeiro dia citado, 2 estavam resfriadas e 7 não estavam resfriadas.
Como 36 pessoas trabalharam no primeiro dia, e 4 x 9 = 36, temos:
Número de pessoas resfriadas: 2 x 4 = 8
Número de pessoas não resfriadas: 7 x 4 = 28
A questão informou que no dia seguinte mais uma pessoa ficou resfriada, de onde concluímos que neste dia haviam 8 + 1 = 9 pessoas resfriadas e 28 – 1 = 27 pessoas não resfriadas.
Nova razão: 9/27 = 1/3.
Resposta: D
Questão 22. No início de um dia, em um escritório, havia 120 envelopes disponíveis para uso, dos quais 37,5% eram amarelos, e os demais, brancos. Sabendo que 20% dos envelopes amarelos e 60% dos envelopes brancos foram utilizados no decorrer do dia, então, o número de envelopes não utilizados nesse dia foi
(A) 64.
(B) 70.
(C) 68.
(D) 62.
(E) 66.
Resolução
Total de envelopes amarelos é 0,375 x 120 = 45
Total de envelopes brancos é 120 – 45 = 75
A questão informou que 20% dos envelopes amarelos foram utilizados, ou seja, 80% deles não foram utilizados. Calculando o total de NÃO utilizados:
0,80 x 45 = 36
A questão também informou que 60% dos envelopes brancos foram utilizados, ou seja, 40% deles não foram utilizados. Calculando o total de NÃO utilizados:
0,40 x 75 = 30
Total de envelopes não utilizados:
36 + 30 = 66.
Resposta: E
Questão 23. Uma máquina, trabalhando 4 horas por dia, produz um lote de peças em 12 dias. Se essa máquina trabalhasse 6 horas por dia, produziria o mesmo lote de peças em
(A) 8 dias.
(B) 10 dias.
(C) 7 dias.
(D) 6 dias.
(E) 9 dias.
Resolução
Questão típica envolvendo regra de três simples.
Perceba que quanto maior a quantidade de horas trabalhadas por dia, menor será a quantidade de dias necessários para o término do lote, ou seja, temos duas grandezas inversamente proporcionais.

6x = 4.12
6x = 48
x = 48/6
x = 8 dias
Resposta: A
Questão 24. Uma pessoa comprou 4 camisetas de valores diferentes, conforme mostra a tabela.
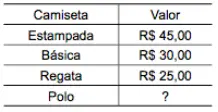
Sabendo que, em média, o valor de cada camiseta foi R$ 40,00, a diferença entre o valor da camiseta mais cara e o da mais barata foi
(A) R$ 35,00.
(B) R$ 20,00.
(C) R$ 30,00.
(D) R$ 15,00.
(E) R$ 25,00.
Resolução
Sabendo que o preço médio das camisas é de R$ 40,00, e que existem 4 camisas, podemos calcular o valor total das camisas:
4 x 40 = R$ 160,00
Calculando o valor da camisa Polo:
160 – 45 – 30 – 25 = R$ 60,00
Camisa mais cara: Polo (R$ 60)
Camisa mais barata: Regata (R$ 25)
Calculando a diferença:
60 – 25 = R$ 35,00
Resposta: A
Questão 25. Um estudante precisa fazer todos os exercícios de uma lista e, para isso, decidiu que irá resolver, por dia, sempre a mesma quantidade de exercícios. Se ele resolver 6 exercícios por dia, levará 3 dias a menos do que levaria se resolvesse 4 exercícios por dia. O número de exercícios da lista é
(A) 48.
(B) 60.
(C) 36.
(D) 72.
(E) 12.
Resolução
Considerando x a quantidade de dias necessários para a resolução da lista, o estudante considerou dois casos: fazer 6 ou 4 exercícios por dia.
Basta resolvermos a equação do primeiro grau 6(x – 3) = 4x, onde 6(x – 3) representa os 6 exercícios por dia, terminando 3 dias antes, e 4x representa 4 exercícios por dia.
6(x – 3) = 4x
6x – 18 = 4x
6x – 4x = 18
2x = 18
x = 18/2
x = 9
Podemos calcular a quantidade total de exercícios através de qualquer um dos lados da equação:
4x = 4.9 = 36
Resposta: C
Questão 26. Em uma caixa há parafusos e pregos, num total de 20 unidades. Sabendo que há 4 parafusos a mais do que o número de pregos, então, o número de parafusos dessa caixa é
(A) 12.
(B) 4.
(C) 8.
(D) 10.
(E) 6.
Resolução
Considere x o número de pregos da caixa. Como existem 4 parafusos a mais do que o número de pregos, podemos concluir que existem x+4 parafusos.
Sabendo que existem 20 unidades no total:
x + x + 4 = 20
2x = 16
x = 8
Total de parafusos:
x + 4 = 8 + 4 = 12
Resposta: A
Questão 27. Para participar de uma festa são cobrados um ingresso de R$ 80,00 e um preço fixo de R$ 6,00 por qualquer tipo de latinha de bebida. Se uma pessoa gastou nessa festa, com o ingresso e as bebidas, um total de R$ 134,00, então o número de latinhas de bebida consumidas por ela foi
(A) 10.
(B) 8.
(C) 6.
(D) 9.
(E) 7.
Resolução
Calculando o total gasto com latinhas:
134 – 80 = R$ 54,00
Sabendo que o preço de cada latinha era de R$ 6,00, podemos calcular a quantidade de latinhas:
54/6 = 9 latinhas.
Resposta: D
Questão 28. Um terreno retangular foi dividido em dois lotes, Ι e ΙΙ, conforme mostra a figura, sendo que as medidas indicadas estão em metros.
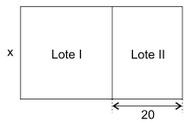
Sabendo que o lote Ι tem a forma de um quadrado com 900 m² de área, então a área total desse terreno é
(A) 1400 m²
(B) 1500 m²
(C) 1200 m²
(D) 1100 m²
(E) 1300 m²
Resolução
Sabendo que o Lote I tem a forma de um quadrado, e que possui 900m², podemos calcular a medida do lado x:
x² = 900
x = √900
x = 30 m
Calculando a área do Lote 2:
30 . 20 = 600 m²
Área total:
900 + 600 = 1500 m²
Resposta: B
Questão 29. Em uma parede foi colocada uma faixa horizontal com azulejos azuis (A) e azulejos brancos (B), obedecendo à seguinte sequência:

Mantendo sempre essa mesma ordem na colocação dos azulejos, isto é, um azulejo azul seguido por dois azulejos brancos, e sabendo que essa faixa terá 57 azulejos, então, o número de azulejos brancos dessa faixa será
(A) 38.
(B) 40.
(C) 42.
(D) 36.
(E) 34.
Resolução
Temos um padrão ABB (três azulejos).
Como 57/3 = 19, temos exatamente 19 repetições ABB.
Se existem 2 azulejos brancos em cada repetição, o total desses azulejos é igual a:
2 . 19 = 38
Resposta: A
Questão 30. Um terreno retangular cujas medidas, em metros, estão indicadas na figura, foi totalmente cercado com um muro.
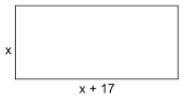
Sabendo que o perímetro desse terreno é 106 metros, então o seu maior lado mede
(A) 31 m.
(B) 22 m.
(C) 27 m.
(D) 18 m.
(E) 35 m.
Resolução
Por definição, perímetro é a soma dos lados.
x + x + x + 17 + x + 17 = 106
4x + 34 = 106
4x = 72
x = 18
Calculando a medida do maior lado:
x + 17 = 18 + 17 = 35 m
Resposta: E
Gostou da prova resolvida (gabarito extraoficial) do segundo concurso da PM SP em 2018?
Deixe o seu comentário.
