Confira aqui a prova resolvida do concurso para a Polícia Militar do Estado do Espírito Santo (PM ES), realizado em 2018 pela AOCP.
Raciocínio Lógico e Matemático.
Boa sorte!
Questão 21. Em um teste de aptidão física de dois soldados, X e Y, um sargento afirmou aos seus superiores que “ou o soldado X foi aprovado ou o soldado Y foi reprovado”.
A negação dessa afirmação é
(A) “O soldado X foi reprovado e o soldado Y foi reprovado”.
(B) “O soldado X foi aprovado ou o soldado Y foi aprovado”.
(C) “O soldado X foi aprovado e o soldado Y foi aprovado”.
(D) “O soldado X foi aprovado se e somente se o soldado Y foi reprovado”.
(E) “Se o soldado X foi reprovado, então o soldado Y foi reprovado”.
Considere:
p: o soldado X foi aprovado
q: o soldado Y foi reprovado
Podemos representar a disjunção exclusiva “ou o soldado X foi aprovado ou o soldado Y foi reprovado” da seguinte forma:
p ⊕ q
Utilizando as equivalências lógicas:
~(p ⊕ q) = p⇔q
Finalizando,
p⇔q: o soldado X foi aprovado se e somente se o soldado Y foi reprovado
Resposta: D
Questão 22. Considere as duas afirmações a seguir:
– Todo soldado atua na defesa civil ou atua na defesa ambiental.
– Pedro é um soldado da defesa civil.
Logo, é correto afirmar que
(A) Pedro atua na defesa civil e na defesa ambiental.
(B) se Pedro não atuar na defesa ambiental, então ele não é um soldado.
(C) Pedro somente atua na defesa ambiental se atuar na defesa civil.
(D) como Pedro atua na defesa civil, então ele também atua na defesa ambiental.
(E) Pedro não atua na defesa ambiental.
Comentário
Pela afirmação 1, um soldado atua na defesa civil ou na defesa ambiental. A afirmação 2, por sua vez, cita que Pedro é um soldado e atua na defesa civil, ou seja, ele não atua na defesa ambiental.
Resposta: E
Questão 23. Se todo soldado é militar e nenhum militar é político, é possível concluir, corretamente, que
(A) nenhum militar é soldado.
(B) nenhum soldado é político.
(C) todo soldado é político.
(D) todo político é militar.
(E) todo militar é soldado.
Comentário
Temos duas afirmações:
– todo soldado é militar
– nenhum militar é político
Podemos reescrever a segunda afirmação da seguinte forma:
Se é militar, então não é político
Daí, como todo soldado é militar, e quem é militar não é político, então podemos concluir nenhum soldado é político.
Resposta: B
Questão 24. Dados os conjuntos A = {1, 2, 3, 4} e B = {3, 4, 5}, então o número de elementos de A∪B é igual a:
(A) 3
(B) 4
(C) 5
(D) 6
(E) 7
Resolução
Os elementos do conjunto A∪B são aqueles que pertencem ao conjunto A ou pertencem ao conjunto B, sem a necessidade de repetição.
A∪B = (1, 2, 3, 4, 5)
Resposta: C
Questão 25. Considere o conjunto C dado por C = {2, 4, 8, x, y}, em que x e y são números inteiros. Sabendo que a soma dos elementos de C resulta em 44 e que o valor de y é o dobro do valor de x, então a diferença entre y e x, nessa ordem, é igual a
(A) 2
(B) 4
(C) 6
(D) 8
(E) 10
Resolução
Sabendo que a soma dos elementos de C é igual a 44, temos:
2 + 4 + 8 + x + y = 44
14 + x + y = 44
x + y = 44 – 14
x + y = 30
Sabendo que o valor de y é o dobro do valor de x, temos:
y = 2x
Substituindo a segunda na primeira equação:
x + y = 30
x + 2x = 30
3x = 30
x = 30/3
x = 10
Calculando o valor de y:
y = 2x
y = 2.10
y = 20
Calculando a diferença:
y – x = 20 – 10 = 10
Resposta: E
Questão 26. O resultado da soma abaixo é um número:
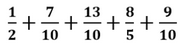
A) divisível por 2.
B) inteiro negativo.
C) divisível por 3.
D) racional e inteiro.
E) racional negativo.
Resolução
Efetuando a adição das frações:
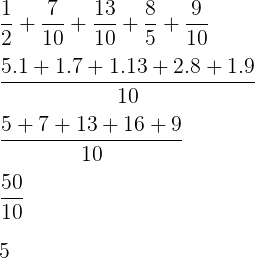
Resposta: D
Questão 27. Em uma ocorrência, foi registrada a apreensão de dois furgões com mercadorias obtidas ilegalmente. No primeiro furgão, foram encontradas 10 caixas da mercadoria A e 12 caixas da mercadoria B, cujo valor total de venda dessas mercadorias resultava em R$ 5.700,00, conforme relatado pelo motorista. No segundo furgão, foram encontradas 20 caixas da mesma mercadoria A e 2 caixas da mesma mercadoria B, cujo valor total de venda dessas mercadorias resultava em R$ 6.340,00, conforme relatado pelo segundo motorista. Considerando que ambos os motoristas falaram a verdade, então o valor de cada caixa do produto B é igual a
A) R$ 230,00.
B) R$ 249,00.
C) R$ 269,00.
D) R$ 280,00.
E) R$ 294,00.
Considere:
a = valor da mercadoria A
b = valor da mercadoria B
No primeiro furgão temos:
10a + 12b = 5700
No segundo furgão temos:
20a + 2b = 6340
O nosso objetivo será resolver o sistema de equações do primeiro grau:
10a + 12b = 5700
20a + 2b = 6340
Dividindo a segunda equação por 2, temos:
10a + 12b = 5700
10a + b = 3170
Subtraindo a segunda da primeira equação:
10a + 12b – 10a – b = 5700 – 3170
11b = 2530
b = 2530/11
b = 230
Resposta: A
Questão28. Se somarmos três unidades ao dobro do número x, obteremos o mesmo resultado que alcançamos ao subtrair duas unidades do triplo do mesmo número x. Dessa forma, o quádruplo do número x é igual a
A) 20.
B) 16.
C) 12.
D) 8.
E) 4.
Resolução
“somarmos três unidades ao dobro do número x”
2x + 3
“subtrair duas unidades do triplo do mesmo número x”
3x – 2
Igualando:
3x – 2 = 2x + 3
3x – 2x = 3 + 2
x = 5
Calculando o quádruplo de x:
4x = 4.5 = 20
Resposta: A
Questão 29. Sejam x e y dois números reais e que estão relacionados pela equação 3y – 2 = x + 15, dessa forma, se x = 10, então o valor de y será igual a
A) 23/3
B) 12.
C) 9.
D) 10.
E) 5.
Resolução
3y – 2 = x + 15
3y – 2 = 10 + 15
3y = 25 + 2
3y = 27
y = 27/3
y = 9
Resposta: C
Questão 30. Das oito horas da manhã até às 16 horas da tarde, o número médio de ligações de emergência diárias para o número 190 pode ser representado pela equação y = x + 15, em que y é o número de chamadas e x é o horário da ligação, considerando somente a hora da ligação, sem os minutos. Por exemplo, às 8h 20min da manhã, o número de ligações será dado por y = 8 + 15 = 23. Nesse período, ficam disponíveis duas viaturas policiais para atender as ligações, sendo que esse número de viaturas disponíveis é dobrado a partir do primeiro horário em que o número de chamadas ultrapassar o valor 28. Dessa forma, o número de viaturas disponíveis é dobrado somente a partir das
(A) 12 horas.
(B) 13 horas.
(C) 14 horas.
(D) 15 horas.
(E) 16 horas.
Resolução
O número de viaturas é dobrado a partir do momento em que o número de chamadas ultrapassar o valor 28.
x + 15 > 28
x > 28 – 15
x > 13
Veja que a hora deve ser superior a 13, ou seja, a frota de viaturas dobrará a partir das 14 horas.
Resposta: C
Está gostando da resolução da prova da PM ES 2018?
Deixe o seu comentário e compartilhe nas redes sociais.
Questão 31. Conforme registros, o número médio de veículos que trafegam em uma determinada rodovia, em determinados horários do dia, é dado pela equação –x² + 24x + 25 = 0, em que x é o horário do registro, começando em 0 e terminando em 24 horas. Dessa forma, o horário do dia em que há o registro do maior número médio de carros trafegando nessa rodovia é
(A) 12 horas.
(B) 13 horas.
(C) 14 horas
(D) 15 horas.
(E) 16 horas.
Resolução
A questão é passível de anulação. Uma equação não consegue representar o número médio de veículos de acordo com o horário do dia.
O correto seria ter apresentado uma função e não uma equação. Possivelmente esta:
f(x) = –x² + 24x + 25
Onde:
a = -1
b = 24
c = 25
Vamos considerar que a banca apresentou a função citada e descobriremos o horário de maior tráfego.
Veja que temos uma função do segundo grau, cujo gráfico é uma parábola (a<0), ou seja, basta descobrirmos o chamado x do vértice:
xv = -b/2a
xv = -24/2(-1)
xv = 12
Resposta: A
Questão 32. 70 soldados se inscreveram em três cursos, em que cada curso é direcionado para uma área de atuação de suas funções: Combate a Incêndio, Busca e Salvamento ou Atendimento Pré-hospitalar. Cada soldado podia optar por se inscrever em um, em dois ou nos três cursos disponibilizados e todos os soldados se inscreveram em pelo menos um dos três cursos oferecidos, da seguinte maneira:
– 59 soldados optaram por cursar Combate a Incêndio;
– 56 soldados optaram por cursar Busca e Salvamento;
– 33 soldados optaram por cursar Atendimento Pré-hospitalar;
– 50 soldados optaram por cursar Combate a Incêndio e Busca e Salvamento;
– 23 soldados optaram por cursar Busca e Salvamento e Atendimento Pré-hospitalar;
– 25 soldados optaram por cursar Atendimento Pré-hospitalar e Combate a Incêndio;
– 20 soldados optaram por cursar as três áreas oferecidas.
Dessa forma, o número de soldados que optaram por cursar somente uma das três áreas de atuação é igual a
A) 7
B) 8
C) 9
D) 10
E) 12
Resolução
Podemos resolver a questão utilizando o Diagrama de Venn.
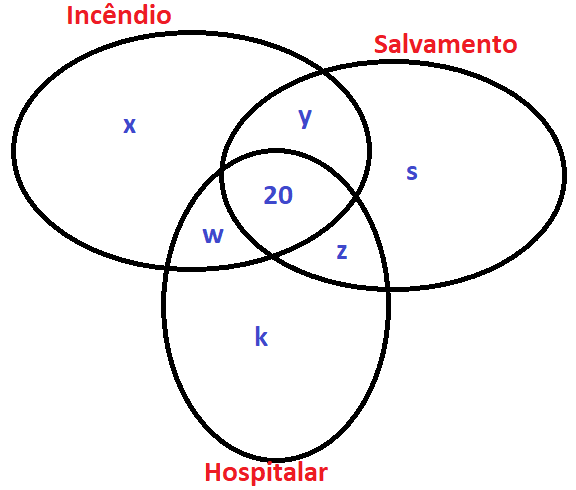
50 soldados optaram por cursar Combate a Incêndio e Busca e Salvamento
y + 20 = 50
y = 50 – 20
y = 30
23 soldados optaram por cursar Busca e Salvamento e Atendimento Pré-hospitalar
20 + z = 23
z = 23 – 20
z = 3
25 soldados optaram por cursar Atendimento Pré-hospitalar e Combate a Incêndio
20 + w = 25
w = 25 – 20
w = 5
Como cada um dos 70 soldados se inscreveu em pelo menos um curso:
x + s + k + y + w + z + 20 = 70
x + s + k + 30 + 5 + 3 + 20 = 70
x + s + k + 58 = 70
x + s + k = 70 – 58
x + s + k = 12
Veja no diagrama que x + s + k representa a quantidade de soldados que se inscreveu em apenas um curso.
Resposta: E
Questão 33. Resolvendo-se a inequação do segundo grau 2x² + 13x – 7 < 0, no conjunto dos números reais (R), obtém-se o conjunto solução S igual a
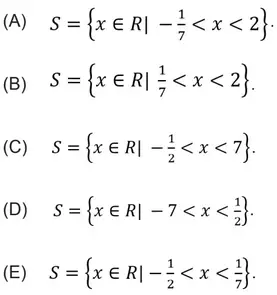
Resolução
Temos uma inequação do segundo grau. A maneira mais fácil de analisar uma equação deste tipo é analisando a função do segundo grau:
f(x) = 2x² + 13x – 7
Onde:
a = 2
b = 13
c = -7
Observe que o gráfico da função é uma parábola côncava para cima, ou seja, os valores de x que fazem f(x)<0 são aqueles que estão entre as raízes da função.
Utilizaremos a fórmula de Bháskara para o cálculo das raízes:
Δ = b² – 4ac
Δ = 13² – 4.2.(-7)
Δ = 169 + 56
Δ = 225
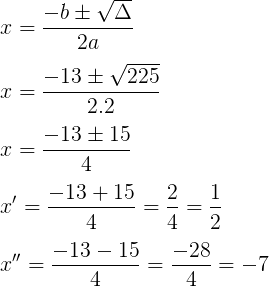
S = {x∈R | -7 < x < 1/2}
Resposta: D
Questão 34. O esboço de gráfico a seguir mostra a relação linear entre o custo y (em reais) da produção de x coletes de segurança:
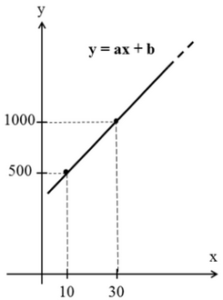
Se forem gastos R$ 2.000,00 na produção de um lote de coletes, então, nesse lote, foram produzidos
A) 70 coletes.
B) 90 coletes.
C) 50 coletes.
D) 80 coletes.
E) 60 coletes.
Resolução
A questão pode ser facilmente resolvida apenas observando no gráfico que a cada aumento de 20 coletes, o custo de produção cresce em 500.
Considerando o ponto (30, 1000), podemos concluir que quando o custo aumenta para 2000, a quantidade de coletes produzida é de 70.
A resolução mais formal seria calcular a equação da reta, considerando que temos dois pontos (10, 500) e (30, 1000).
Para tanto, basta resolvermos o sistema de equações do primeiro grau:
500 = 10a + b
1000 = 30a + b
Resolvendo o sistema, temos:
a = 25
b = 250
A equação reduzida da reta será:
y = 25x + 250
Considerando y = 2000:
2000 = 25x + 250
25x = 2000 – 250
25x = 1750
x = 1750/25
x = 70
Resposta: A
Questão 35. Considerando a palavra SOLDADO, é correto afirmar que
(A) é possível formar 360 anagramas dessa palavra que começam pela letra L.
(B) é possível formar 720 anagramas dessa palavra que começam pela letra D.
(C) é possível formar 5040 anagramas dessa palavra, no total.
(D) é possível formar 24 anagramas dessa palavra que começam com a letra D e terminam com a letra O.
(E) é possível formar 12 anagramas dessa palavra que terminam com as letras SOL, nessa ordem.
Resolução
Quantidade de anagramas que começam com a letra L.
L _ _ _ _ _ _ (duas letras D e duas letras O)
6! / 2!2! = 180
Quantidade de anagramas que começam com a letra D.
D _ _ _ _ _ _ (duas letras O)
6! / 2! = 360
Quantidade total de anagramas.
_ _ _ _ _ _ _ (duas letras D e duas letras O)
7! / 2!2! = 1260
Quantidade de anagramas que começam com D e terminam com O.
D _ _ _ _ _ O
5! = 120
Quantidade de anagramas que terminam com SOL.
_ _ _ _ S O L (duas letras D)
4! / 2! = 12
Resposta: E
Questão 36. Considere as duas matrizes abaixo.
![]()
Sendo C uma nova matriz tal que C = 3B – 2A, então a soma dos elementos da matriz C é igual a
(A) 5.
(B) 10.
(C) 15.
(D) 20.
(E) 25.
Resolução
Calculando os elementos da matriz C:
c11 = 3.8 – 2.1 = 24 – 2 = 22
c12 = 3.2 – 2.8 = 6 – 16 = -10
c21 = 3.1 – 2.1 = 3 – 2 = 1
c22 = 3.2 – 2.2 = 6 – 4 = 2
Somando os elementos de C:
22 – 10 + 1 + 2 = 15
Resposta: C
Questão 37. Considere as duas matrizes A e B a seguir:
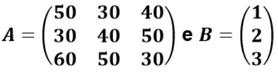
Cada linha da matriz A indica a pontuação obtida, em cada tentativa, em uma prova de tiro ao alvo por um competidor. Assim, a primeira linha indica as pontuações do competidor X, a segunda linha indica as pontuações do competidor Y e a terceira linha indica as pontuações do competidor Z. Obtendo-se uma matriz C = A.B, na matriz C aparece a nota de desempenho final de cada um dos três competidores X, Y e Z, respectivamente, na primeira, na segunda e na terceira linha. Dessa forma, é correto afirmar que
(A) o competidor X obteve a menor nota de desempenho final, igual a 250.
(B) o competidor Y obteve a maior nota de desempenho final, igual a 260.
(C) o competidor Z obteve a menor nota de desempenho final, igual a 230.
(D) os competidores X e Y obtiveram a mesma nota de desempenho final.
(E) os competidores X e Z obtiveram a mesma nota de desempenho final.
Resolução
Calculando a nota de cada um dos competidores:
X = 50.1 + 30.2 + 40.3 = 50 + 60 + 120 = 230
Y = 30.1 + 40.2 + 50.3 = 30 + 80 + 150 = 260
Z = 60.1 + 50.2 + 30.3 = 60 + 100 + 90 = 250
Resposta: B
Questão 38. Para saber o custo total (em reais) na produção de x uniformes para um grupo de soldados, primeiramente substitui-se cada elemento x, da matriz a seguir, pela quantidade de uniformes que se quer produzir e calcula-se o determinante dessa matriz, obtendo-se, assim, o custo total na produção destes x uniformes igual ao valor do determinante.
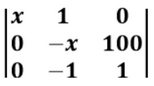
Dessa forma, para se produzir 70 uniformes para um grupo de soldados, o custo total nessa produção será de
(A) R$ 4.100,00.
(B) R$ 3.500,00.
(C) R$ 3.100,00.
(D) R$ 2.500,00.
(E) R$ 2.100,00.
Resolução
Calculando o determinante:
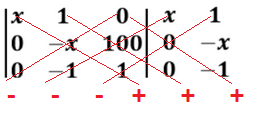
Det = x.(-x).1 + 1.100.0 + 0.0.(-1) – 0.(-x).0 – (-1).100.x – 1.0.1
Det = -x² + 100.x
Quando x = 70, temos:
Det = -70² + 100.70
Det = -4900 + 7000
Det = 2100
Resposta: E
Questão 39. Sobre uma mesa, estão dois recipientes: o primeiro tem um formato de um cubo, tal que cada aresta desse cubo mede x cm; o segundo tem o formato de um paralelepípedo reto, cujas dimensões são 5 cm, 25 cm e 125 cm. Sabendo que os dois recipientes possuem o mesmo volume, então a medida da aresta x do cubo é igual a
(A) 5 cm.
(B) 12 cm.
(C) 25 cm.
(D) 50 cm.
(E) 125 cm.
Volume do recipiente em formato de cubo:
V = x³
Volume do recipiente em formato de paralelepípedo reto:
V = 5.25.125 = 15625
Como os recipientes possuem o mesmo volume:
x³ = 15625
x = 25
Resposta: C
Questão 40. Em uma loja especializada em vestuário e calçados para militares, estão sendo anunciados três tipos de compra:
• Na compra de 2 coturnos, 1 farda e 3 quepes, o cliente irá pagar R$ 770,00;
• Na compra de 1 coturno, 2 fardas e 3 quepes, o cliente irá pagar R$ 850,00;
• Na compra de 1 coturno, 3 fardas e 2 quepes, o cliente irá pagar R$ 840,00.
Independentemente se o cliente vai aceitar ou não uma dessas ofertas, os preços de cada item citado são fixos e não mudam, mesmo que o cliente faça outra escolha nas quantidades de cada item. Dessa forma, caso um cliente queira comprar somente 1 coturno, 1 farda e 1 quepe, ele irá pagar por essa compra a quantia de
(A) R$ 380,00.
(B) R$ 450,00.
(C) R$ 930,00.
(D) R$ 910,00.
(E) R$ 600,00.
Considere:
x = preço do coturno
y = preço da farda
z = preço do quepe
Analisando as três situações, temos três equações:
(1) 2x + y + 3z = 770
(2) x + 2y + 3z = 850
(3) x + 3y + 2z = 840
Fazendo (2) – (3):
x + 2y + 3z – x – 3y – 2z = 850 – 840
z – y = 10
Fazendo (1) – 2*(3):
2x + y + 3z – 2x – 6y – 4z = 770 – 1680
– 5y – z = – 910
Somando as duas equações encontradas:
z – y – 5y – z = 10 – 910
-6y = -900
y = 900/6
y = 150
Calculando o valor de z:
z – y = 10
z – 150 = 10
z = 150 + 10
z = 160
Calculando o valor de x:
x + 2y + 3z = 850
x + 2.150 + 3.160 = 850
x + 300 + 480 = 850
x + 780 = 850
x = 850 – 780
x = 70
Valor de 1 coturno, 1 farda e 1 quepe:
x + y + z = 70 + 150 + 160 = 380
Resposta: A
Gostou da prova resolvida da PM ES 2018?
Deixe o seu comentário.

Contando as 20 questões, consegui 14 🙂
Parabéns Olavo!
Muito obrigada!! Fico feliz por disponibilizar gratuitamente a resolução da prova e tbm os conteúdos matemáticos!!!