Olá! Procurando exercícios resolvidos sobre funções quadráticas, também conhecidas como funções do segundo grau? Confira aqui uma seleção especial de questões, todas de provas de concursos públicos realizados nos últimos anos. Caso tenha dúvidas, consulte o nosso material didático.
Bom estudo!
Questão 1 (PC MG – Acadepol). O número de ocorrências registradas das 12 às 18 horas em um dia do mês de janeiro, em uma delegacia do interior de Minas Gerais, é dado por f(t) = – t² + 30t – 216, em que 12 ≤ t ≤ 18 é a hora desse dia. Pode-se afirmar que o número máximo de ocorrências nesse período do dia foi
A) 0
B) 9
C) 15
D) 18
Resolução:
Temos que a função quadrática f(t) = – t² + 30t – 216 tem como gráfico uma parábola com a concavidade para baixo (a é menor que 0).
Assim sendo, o t que faz a função ser máxima é justamente o t do vértice, que pode ser calculado utilizando a fórmula abaixo:
tv = -b/2a = -30/2(-1) = 15
Logo, t = 15 horas foi o momento de maior número de ocorrências.
Como já sabemos o momento de maior ocorrência, vamos agora calcular t(15):
t(15) = – 15² + 30.15 – 216
t(15) = -225 + 450 – 216
t(15) = 9 ocorrências.
Obs: Outra opção seria calcular o y do vértice pela fórmula yv = – Δ/4a.
Resposta: B
Observação: Devido a grande quantidade de dúvidas sobre o valor de -15², publicamos uma página especial sobre o assunto. Clique aqui para acessá-la.
Questão 2 (CFO PM ES – Exatus). Uma agência de viagens vende pacote turísticos coletivos com destino a Fortaleza. Um pacote para 40 clientes custa R$ 2000,00 por pessoa e, em caso de desistência, cada pessoa que permanecer no grupo deve pagar mais R$ 100,00 por cada desistente do pacote de viagem. Dessa forma, para que essa agência obtenha lucro máximo na venda desse pacote de viagens, o número de pessoas que devem realizar a viagem é igual a:
a) 30
b) 20
c) 25
d) 28
e) 50
Resolução:
Sendo x a quantidade de pessoas, o preço total é dado pela quantidade de pessoas vezes o preço por pessoa, que é 2000 mais 100 por desistente.
C(x) = x(2000 + 100(40 – x))
C(x) = x(2000 + 4000 – 100x)
C(x) = x(6000 – 100x)
C(x) = 6000x – 100x²
Temos uma função do segundo grau.
Vamos calcular as raízes:
6000x – 100x² = 0
60x – x² = 0
x(60 – x) = 0
Assim, x = 0 ou x = 60
Como em nossa função o valor de a = -100 < 0, o gráfico é uma parábola para baixo, portanto possui valor máximo, e é exatamente o valor entre as raízes 0 e 60, portanto o valor máximo ocorre quando x = 30.
Resposta: Resposta: A
Questão 3 (PM ES – Exatus). Assinale a alternativa correta:
a) O gráfico da função y = x² + 2x não intercepta o eixo y.
b) O gráfico da função y = x² + 3x + 5 possui concavidade para baixo.
c) O gráfico da função y = 5x – 7 é decrescente.
d) A equação x² + 25 = 0 possui duas raízes reais e diferentes.
e) A soma das raízes da função y = x² – 3x – 10 é igual a 3.
Resolução
a) FALSA: Uma parábola sempre intercepta o eixo y.
b) FALSA: O valor de a = 1 >0. Concavidade para cima.
c) FALSA: O valor de a = 5 > 0. Crescente.
d) FALSA: Nenhum número Real elevado ao quadrado fica negativo.
e) VERDADEIRA
Lembrando da fórmula da soma das raízes:
Soma = -b/a = -(-3)/1 = 3
Resposta: E
Questão 4 (PM ES – Funcab). Dada a função quadrática f(x) = -2.x² + 4.x – 9, as coordenadas do vértice do gráfico da parábola definida por f(x), é:
A) V = (-7; 1)
B) V = (1; -7)
C) V = (0; 1)
D) V = (-7; 0)
E) V = (0; 0)
Resolução:
Considerando que trata-se de uma função quadrática, vamos utilizar a fórmula do x do vértice:
xv = -b/2a = -4/2(-2) = 4/4 = 1
Para calcular o y, basta utilizar x=1:
y = -2.1 + 4.1 – 9 = -2 + 4 – 9 = -7
Clique aqui para assistir a resolução
Resposta: B
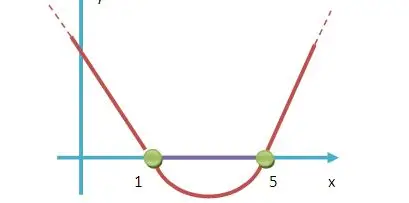
Questão 5 (PM ES – Funcab). Uma festa no pátio de uma escola reuniu um público de 2.800 pessoas numa área retangular de dimensões x e x + 60 metros. O valor de , em metros, de modo que o público tenha sido de, aproximadamente, quatro pessoas por metro quadrado, é:
A) 5 m
B) 6 m
C) 8 m
D) 10 m
E) 12 m
Resolução:
A área de um retângulo é calculada multiplicando-se a base pela altura.
Temos:
Área = x.(x + 60)
Área = x² + 60x
Como existem 2800 pessoas e queremos 4 pessoas por m²:
4.(x² + 60x) = 2800
4x² + 240x = 2800
4x² + 240x – 2800 = 0
Dividindo todos os membros por 4:
x² + 60x – 700 = 0
Utilizando as fórmulas de soma e produto:
Soma das raízes = -b/a = -60
Produto das raízes: c/a = -700
É fácil observar que as raízes são 10 e -70. Como x representa medida, descartamos o -70, e a resposta será 10 m.
Resposta: D
Questão 6 (PM Acre – Funcab). Determine o valor de x que provoca o valor máximo da função real f(x) = -x² + 7x – 10.
A) 3,5
B) – 2
C) 0
D) 10
E) – 1,5
Resolução:
Como temos uma função quadrática, vamos achar as raízes pelo método de soma e produto:
a = -1, b = 7, c = -1
Soma = -b/a = -7/-1 = 7
Produto = -10/-1 = 10
Dois números cuja soma é 7 e o produto é 10. As raízes são 2 e 5.
O valor máximo (pois a é negativo) é a média das raízes:
(2 + 5)/2 = 7/2 = 3,5
Resposta: A
Questão 7 (PM Acre – Funcab). Sabendo que uma função quadrática possui uma raiz igual a -2 e que obtém seu valor máximo quando x = 5, determine o valor da outra raiz dessa função.
A) 3
B) 7
C) 10
D) 12
E) 15
Resolução:
Basta sabermos o valor de x que faz a função quadrática ter um valor máximo é a média aritmética das raízes:
Considerando que as raízes são -2 e k, e que a média deles é 5, temos:
(-2 + k)/2 = 5
-2 + k = 10
k = 10 + 2
k = 12
Resposta: D
Questão 8 (PM Pará). Uma empresa criou o modelo matemático L(x)=-100x²+1000×-1900 para representar o lucro diário obtido pela venda de certo produto, na qual x representa as unidades vendidas. O lucro máximo diário obtido por essa empresa é igual a:
a) R$600,00
b) R$700,00
c) R$800,00
d) R$900,00
e) R$1.000,00
Resolução:
Como temos uma função do segundo grau, onde a é negativo, basta calcularmos o y do vértice, pois este será o máximo da função:
Pela fórmula:
y do vértice = – Δ/4a
Vamos primeiro calcular o valor de Δ:
Δ = b² – 4.a.c = 1000² – 4.(-100).(-1900) = 1000000 – 760000 = 240000
yv = -Δ/4a = -240000/4.(-100) = 240000/400 = 600
Resposta: A
Gostou dos nossos exercícios resolvidos sobre função quadrática?
Deixe o seu comentário.
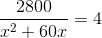
eu estava observando, mas posso estar enganada, -15² pra mim, é 225 pois a conta seria -15 x -15 e – com – da + (questão numero 12 vulgo a primeira das funções quadráticas)
Giovanna,
Você estaria correta se fosse (-15)² = (-15).(-15) = 225
Como não temos os (), -15² = -(15.15) = -225
Bons estudos!
Jordon, Giovanna está correta, pois quando se eleva um número negativo a um expoente par, o sinal sai. bjs. bons estudos!
Desculpe Júlia, a resolução está correta.
Veja os exemplos:
(-3)² = 9
-3² = -9
Bons estudos.
Entao a calculadora tambem errou, pois ja fiz isso 300 vezes e nenhum da negativo.
Olá Luiz!
Sugiro que procure um professor de matemática para uma explicação mais detalhada.
A calculadora realmente não erra, talvez esteja inserindo informações de forma equivocada.
Abraço.
Se esta dentro do parênteses eleva o numero com o sinal ao quadrado e – com – é +.
Mas como está sem parênteses ele o número ao quadrado e mantem o sinal de –
Não encham, Jordon que está certo!!!
Giovanna, você esta correta.
giovanna, perceba que na equação existe -1.x**2, então encare como: -1. (15**2)
Giovanna está correta pois todo numero negativo elevado ao quadrado ele fica positivo. Agora se o numero fosse elevado a algum outro numero IMPAR ele ficaria negativo.
E em relação ao Jordon ele está errado pois se tem o parênteses nos números -(15.15) o sinal de menos (-) está nos dois números 15. -(15.15) = (-15).(-15) = 225.
Desculpe-me Gustavo mas a resolução está correta.
Veja como a ausência dos parênteses faz toda a diferença:
-15² = -(15.15) = -225
(-15)² = (-15).(-15) = 225
Desculpe devemos saber que -15^2 é diferente de (15)^2 bons estudos
Seria muito mais interessante se esses exercicios fossem resolvidos passo a passo.
A primeira questão está com a resolução e o gabarito errada, pela interpretação não se calcula o X do vértice e sim o Y pois a função é dada em f(t), ou seja o Y do vértice que no caso seria “9” através da fórmula – Δ/4a
Natan, favor verificar pois a resposta foi justamente 9 ocorrências.
qual segredo da funções quadraticas?????
Olá Arlequim,
O segredo é estudar e praticar bastante… rs
11) Dada a função f(x) = -(x – 5)2 – 7, analisar os itens
abaixo:
I – O número de raízes inteiras é igual a 0.
II – A concavidade da parábola é voltada para cima.
III – Uma das raízes inteiras é 5.
Está(ão) CORRETO(S):
a) Somente o item I.
b) Somente o item II.
c) Somente os itens I e III.
d) Somente os itens II e III.
Alguem resolve? qual a resposta correta?
Ana Paula,
Imagino que a função seja F(X)= -(x-5)^2 – 7.
Simplificando temos:
F(x)= -x^2 + 10x – 32
Como a<0 e ∆<0, a parábola é côncava para baixo e não possui raíz real.
ENTAO QUAL A RESPOSTA ESTA CORRETA, NAO INTENDI A RESOLUÇÃO DA QUESTAO.
Ana,
Pelas conclusões acima, podemos descartar os itens II e III
I – O número de raízes inteiras é igual a 0.
II – A concavidade da parábola é voltada para cima.
III – Uma das raízes inteiras é 5.
A única certa é a I, pois como não possui raízes reais, não possui raízes inteiras.
Parabéns Jordon!
Pelos comentários acima, antes de estudar função quadrática, o pessoal deveria estudar potenciação e radiciação.
Abraço.
Eu acho graça é que ainda teimam com uma coisa simples.
(-2)²=(-2*-2)=4
-2² = -(+2)², ou seja, -(2*2) = -4
e antes que alguém diga que positivo * negativo = negativo, vale lembrar que primeiro se resolve potenciação e radiciação, depois multiplicação e divisão, e por fim adição e subtração.
o que eu acho mais engraçado são pessoas teimando com um MESTRE em matemática por uma Universidade Federal.
Olá alguem poderia me ajudar. Determine os zeros reais da função f(x)= x² – √2+ 1/2
no 1° questão o xv já não era a resposta ?
Mateus, o t(v) representa o período onde o número de ocorrências é maior. Para acharmos esse número máximo, precisamos calcular o y(v).
Com base nestes conhecimentos podemos calcular qual e o valor maximo ou minimo de uma funcao quadratica .
Alguém por favor me explica a 5 questão detalhadamente, ainda não capitei o por que dá 10 sendo que as raízes são -700 e -60
Olá Nalanda!
As raízes não são -700 e -60.
Pelas fórmulas da soma e do produto das raízes nós concluímos que se somarmos as raízes, o resultado será igual a -60, e se multiplicarmos as raízes, o resultado será igual a -700.
Veja que:
-70 + 10 = -60
-70.10 = -700
Daí, podemos concluir que as raízes são -70 e 10.
É fácil observar que as raízes são 10 e -70. Como x representa medida, descartamos o -70, e a resposta será 10 m.
Gostaria muito que colocassem mais exercicios de funçoes afim
Parabéns, Jordon! Estou procurando material para trabalhar com meus alunos e os seu material foi de grande valia.
É duro trabalhar com educação neste momento, disponibilizar material e de volta receber críticas de pessoas que nem sabem matemática e vem dizer que você está errado.
Parabéns pelo seu trabalho, que Deus te ilumine em sua caminhada.
Os Bolsominions do passado. rsrsrs