Nesta página aprenderemos um pouco sobre a função quadrática. Veremos a definição, a representação gráfica, a famosa parábola, e muitos exemplos.

É muito importante que você aprenda sobre este tipo de função, que costuma cair em 99% dos concursos e vestibulares. Não se esqueça também de estudar através dos exercícios resolvidos.

Bons estudos!

Introdução

Uma função é dita quadrática ou do 2º grau quando é do tipo:

f: R → R

f(x) = ax² + bx + c.

Observe que o valor de “a” não pode ser zero, caso contrário, não seria uma função quadrática e sim afim. Essa restrição é apenas para o valor de “a”, pois b e c podem ser iguais a zero perfeitamente, pois mesmo assim a função continuará sendo quadrática.

Exemplos de funções quadráticas

f(x) = 8x² – 4x  + 1, onde a = 8, b = – 4 e c = 1

f(x) = x² -11, onde a = 1, b = 0 e c = -11

f(x) = 2x² + 32x + 5, onde a = 2, b = 32 e c = 5

f(x) = – x² + 0,8x, onde a = -1, b = 0,8 e c = 0

f(x) = -3,4x², onde a = – 3,4, b = 0 e c = 0

f(x) = 2,34x² + 3,2x + 0,05, onde a = 2,34, b = 3,2 e c = 0,05

f(x) = x² + x + 1, onde a = 1, b = 1 e c = 1

Gráfico

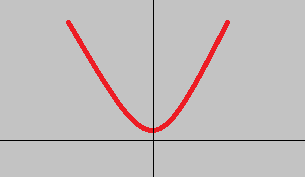
O gráfico de uma função quadrática é uma curva denominada parábola. Veja a figura abaixo:

• O coeficiente “a”

Quando queremos construir um gráfico de uma função quadrática, uma das primeiras informações que temos que observar é o coeficiente a. Veja:

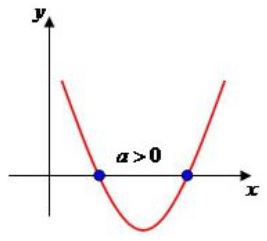
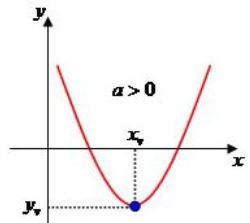
• Se o coeficiente a>0, a concavidade da parábola é para cima.
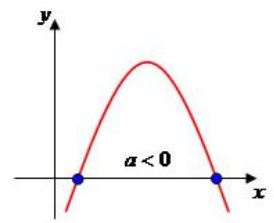
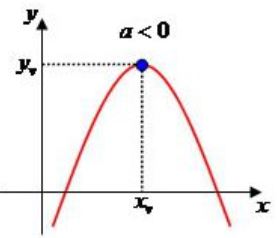
• Se o coeficiente a<0, a concavidade da parábola é para baixo.

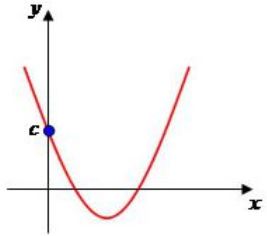
• O coeficiente “c”

A letra c também nos dá uma informação muito importante. Com ela sabemos onde a parábola corta o eixo y. Veja:

Construção do gráfico

Seja a função f(x) = x² + 2x – 3. Com o que aprendemos até agora, sabemos que:

• Como f é uma função quadrática, o gráfico é uma parábola.
• Como a>0 (a=1), a concavidade é para cima.
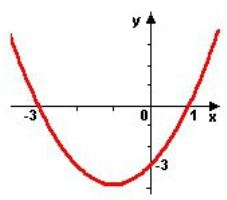
• Como c = -3, a parábola corta o eixo y no ponto (0, -3).

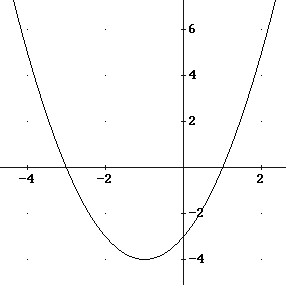
Construindo o gráfico com essas informações, temos:

Zeros da função quadrática

Para o gráfico ficar completo, existe uma informação muito importante que precisamos descobrir. Os chamados zeros, ou raízes, da função, ou seja, os valores de x que fazem f(x)=0.

E como poderemos achar esses valores? Com certeza você já deve ter ouvido falar da famosa fórmula de Bhaskara não é mesmo? O jeito mais fácil de achar as raízes de uma função quadrática é através dela.

Esse cálculo será feito em duas etapas:

Seja a função f(x) = ax² + bx + c

Primeiro devemos calcular o valor de Δ (delta):

Δ = b² – 4ac

Depois calculamos as raízes através da fórmula:

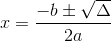
Vamos Praticar?

Vamos aproveitar que aprendemos a calcular as raízes da função quadrática e calcular para o nosso exemplo anterior f(x) = x² + 2x – 3.

Temos que a=1, b=2 e c=-3.

Calculando o valor de Δ:

Δ = b² – 4ac

Δ = 2² – 4.1.(-3)

Δ = 4 + 12

Δ = 16

Calculando as raízes:

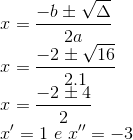
Logo, o gráfico da função f passa pelos pontos (-3, 0) e (1, 0).

O discriminante Δ

O valor de Δ (delta) também nos dá uma informação muito importante. Ele nos informa quantas raízes a função f possui. Veja:

• Se Δ<0, a parábola não corta o eixo x e não possui raízes reais.
• Se Δ=0, a parábola corta o eixo x em apenas um ponto e possui apenas uma raiz real.
• Se Δ>0, a parábola corta o eixo x em dois pontos distintos e possui duas raízes reais.

O vértice da parábola

Já descobrimos o formato do gráfico de uma função quadrática, onde esse gráfico corta os eixos x e y, basta agora descobrirmos as coordenadas do vértice, ou seja, o ponto de valor máximo, quando a < 0, ou o ponto mínimo, quando a < 0. Veja:

O cálculo não é complicado e pode ser feito através das fórmulas abaixo:

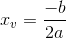
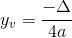
Vamos praticar?

Mais uma vez vamos utilizar o exemplo f(x) = x² + 2x – 3, onde Δ=16, a=1, b=2 e c=-3.

Utilizando as fórmulas:

Xv = -b/2a = -2/2 = -1

Yv = -Δ/4a = -16/4 = -4

Daí, a localização do vértice será no ponto (-1, -4).

Veja no gráfico do nosso exemplo que o resultado é compatível.

Gostou do nosso conteúdo sobre função quadrática?

Deixe o seu comentário.