Olá caros estudantes. Nesta página vamos aprender a utilizar o famoso Teorema de Laplace, muito útil para o cálculo de determinantes de matrizes 4×4, ou de ordem superior.
Não deixe de ler primeiro os nossos conteúdos sobre matrizes e determinantes para evitar queimar etapas.
Bom estudo!
COFATOR
Antes de falarmos sobre o Teorema de Laplace, vamos aprender a calcular o cofator.
Seja A uma matriz de ordem maior ou igual a 3. Vamos representar o cofator de um elemento aij qualquer de A por Aij, onde 1≤i e j≤n.
Definimos:
Aij = (-1)i+j.Dij, onde Dij é o determinante que se obtém de A, eliminando a i-ésima linha e a j-ésima coluna.
Exemplo 1:
Calcular o cofator dos elemento a13, a22 e a33 da matriz abaixo.
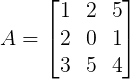
![]()
![]()
![]()
TEOREMA DE LAPLACE
Para calcular o determinante de uma matriz quadrada de ordem n através do Teorema de Laplace, basta seguirmos os dois passos abaixo:
- Escolher arbitrariamente uma linha (ou coluna) da matriz.
- Somar os produtos dos elementos dessa linha (ou coluna) pelos respectivos cofatores.
Como foi falado, não importa a linha ou coluna escolhida, o valor do determinante será sempre o mesmo.
Vale ressaltar que este teorema pode ser aplicado a matrizes de qualquer ordem, porém existem ferramentas mais simples para os determinantes de matrizes 2×2 e 3×3.
Exemplo 2:
Vamos utilizar o Teorema de Laplace para calcular o determinante da matriz A(4×4) abaixo:
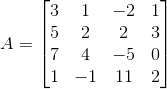
Como podemos escolher qualquer linha ou coluna, vamos escolher a linha 3.
DetA = 7.A31 + 4.A32 + (-5).A33 + 0.A34
Calculando os cofatores, onde omitiremos os cálculos dos determinantes das matrizes 3×3:
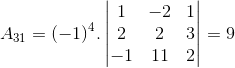
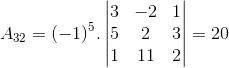
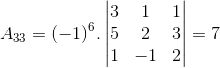
DetA = 7.9 + 4.20 + (-5).7 + 0 = 108

Pingback: Cofator – Saber Matemática