Você sabe o que são as Relações de Girard? Veremos aqui a definição e como elas se aplicam na resolução de equações polinomiais.
Bom estudo!
Relações de Girard em equações do segundo grau
O exemplo mais simples de Relações de Girard é o famoso método da soma e do produto.
Através dele é possível descobrir as raízes de equações do segundo grau sem a necessidade da fórmula de Bhaskara.
Seja ax² + bx + c = 0 uma equação do segundo grau qualquer com a, b e c ∈ R e a ≠ 0.
Considerando que as raízes são r1 e r2, temos que:
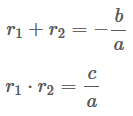
Relações de Girard em equações do terceiro grau
Seja ax³ + bx² + cx + d = 0 uma equação do segundo grau qualquer com a, b, c e d ∈ R e a ≠ 0.
Considerando que as raízes são r1, r2, e r3, temos que:
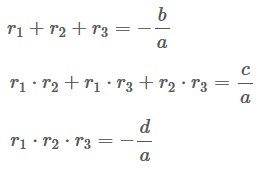
Relações de Girard em equações do quarto grau
Seja ax + bx³ + cx² + dx + e = 0 uma equação do segundo grau qualquer com a, b, c, d e e ∈ R e a ≠ 0.
Considerando que as raízes são r1, r2, r3 e r4, temos que:
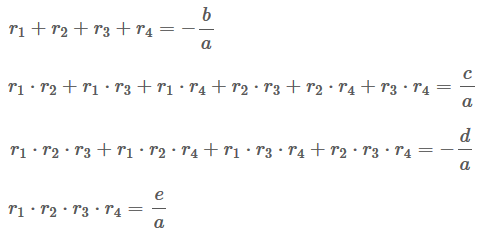
Gostou da nossa publicação sobre as Relações de Girard?
Deixe o seu comentário.
Trackbacks/Pingbacks