Você sabe calcular as raízes de uma equação do segundo grau através do método da soma e do produto? Veja aqui as fórmulas e vários exemplos.
Bom estudo!
Definição
Seja ax² + bx + c = 0 uma equação do segundo grau qualquer com a, b e c ∈ R e a ≠ 0.
A soma das raízes pode ser calculada através da seguinte fórmula:
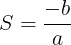
O produto das raízes pode ser calculado através da seguinte fórmula:
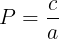
Esse método é muito útil para encontrarmos as raízes de forma mais ágil, sem a necessidade da utilização da fórmula de Bhaskara.
O ponto negativo é que este método é efetivo apenas para algumas equações, principalmente as que possuem raízes inteiras.
Exemplo 1. Encontrar as raízes da equação x² – 3x + 2 = 0.
Observe que:
- a = 1
- b = – 3
- c = 2
Calculando a soma das raízes:
S = -b/a = -(-3)/1 = 3
Calculando o produto das raízes:
P = c/a = 2/1 = 2
Basta agora descobrimos os dois números cuja soma é igual a 3 e o produto é igual a 2.
Para facilitar, a dica é sempre começar pelo produto.
Quais são os números cujo produto é igual a 2?
O par 1 e 2 é uma possibilidade.
Veja que a soma também é igual a 3, ou seja, descobrimos as raízes da nossa equação.
O conjunto solução é dado por S = {1, 2}.
Exemplo 2. Calcular as raízes da equação x² – 5x + 6 = 0.
Observe que:
- a = 1
- b = – 5
- c = 6
Calculando a soma das raízes:
S = -b/a = -(-5)/1 = 5
Calculando o produto das raízes:
P = c/a = 6/1 = 6
Sabendo que a soma é igual a 5, temos algumas possibilidades triviais:
1 + 4 = 5
2 + 3 = 5
Testando as duas possibilidades, sabendo que o produto deve ser igual a 6:
1 . 4 = 4
2 . 3 = 6
Veja que o conjunto solução é S = {2, 3} pois 2 + 3 = 5 e 2 . 3 = 6.
Aprendeu a calcular as raízes de uma equação do segundo grau através do método da soma e do produto?
Deixe o seu comentário.
Trackbacks/Pingbacks