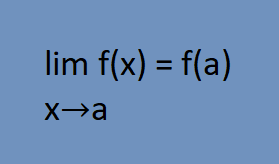Dando início a nossa série de posts sobre o estudo das derivadas, falaremos aqui sobre as funções contínuas, onde apresentamos a definição e vários exemplos.
Não deixe de ver também as nossas publicações sobre outros tópicos do cálculo numérico.
Bom estudo!
DEFINIÇÃO DE FUNÇÃO CONTÍNUA
Podemos dizer que uma função contínua é aquela cujo gráfico pode ser desenhado sem tirar o lápis do papel. Para facilitar a compreensão, veremos alguns exemplos de funções que apresentam “anomalias” que impedem o seu desenho contínuo.
Exemplo 1. Analisar a função abaixo, definida em R – {3}.
Para x ≠ 3, temos:
Vejamos o gráfico da função f:
Como não existe f(3), o gráfico de f apresenta um “furo” no ponto (3, 6).
Dizemos que a função é descontínua em x=3.
Exemplo 2. Analisar a função abaixo, definida em R*.
Para x ≠ 0, temos:
- se 2x<0, f(x) = -2x/x = -2
- se 2x>0, f(x) = 2x/x = 2
Vejamos o gráfico da função f:
Veja que a função não está definida no ponto x = 0, onde apresenta um “degrau”.
Dizemos que a função é descontínua em x=0.
Exemplo 3. Analisar a função abaixo, definida em R – ]1, 2[.
f(x) = x – 2, se x>2;
f(x) = -x + 1, se x<1.
Vejamos o gráfico da função f:
Veja que a função não está definida quando x está entre 1 e 2. Existe um “espaço” entre esses dois números.
Dizemos que a função é descontínua no intervalo real ]1, 2[.
CONCLUSÕES
Nos três exemplos apresentamos gráficos com anomalias (furo, degrau e espaço). Essas anomalias são chamadas de pontos de descontinuidade.
- Uma função cujo gráfico não apresenta anomalias para todo x∈R é chamada de função contínua.
- Uma função cujo gráfico não apresenta anomalias no intervalo ]a, b[ é dita contínua em ]a, b[.
São exemplos de funções contínuas:
- funções polinomiais;
- funções seno e cosseno;
- funções exponenciais.
UTILIZANDO CONCEITOS DE LIMITES
Podemos dizer que uma função f é contínua em um ponto x=a se valer a seguinte condição:
Veja que uma função é contínua em x=a se o limite existe e é igual a f(a), ou seja, f(a) também existe.
Exemplo 4. A função f(x) = x² é contínua para todo x∈R.
Veja que o gráfico não possui nenhum tipo de anomalia.
Também é fácil verificar que o limite é igual a f(a) para todo x=a.
Gostou da nossa página sobre as funções contínuas?
Deixe o seu comentário.