Estudando matemática e estatística para concursos? Confira aqui vários exercícios resolvidos sobre variância e desvio padrão, todos retirados de provas oficiais.
Bom estudo!
Exercício 1 (FCC). Ao considerar uma curva de distribuição normal, com uma média como medida central, temos a variância e o desvio padrão referentes a esta média. Em relação a estes parâmetros,
a) a variância é uma medida cujo significado é a metade do desvio padrão.
b) a variância é calculada com base no dobro do desvio padrão.
c) o desvio padrão é a raiz quadrada da variância.
d) a média dividida pelo desvio padrão forma a variância.
e) a variância elevada ao quadrado indica qual é o desvio padrão.
Resolução
O desvio padrão é a raiz quadrada da variância.
Veja a fórmula:
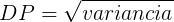
Resposta: C
Exercício 2 (FGV). Os dados a seguir são as quantidades de empregados de cinco pequenas empresas: 6, 5, 8, 5, 6. A variância da quantidade de empregados dessas cinco empresas é igual a:
a) 0,8
b) 1,2
c) 1,6
d) 2,0
e) 2,4
Resolução
O primeiro passo será calcular a média aritmética:
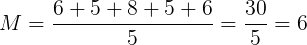
Sabendo o valor da média, podemos calcular o valor da variância:
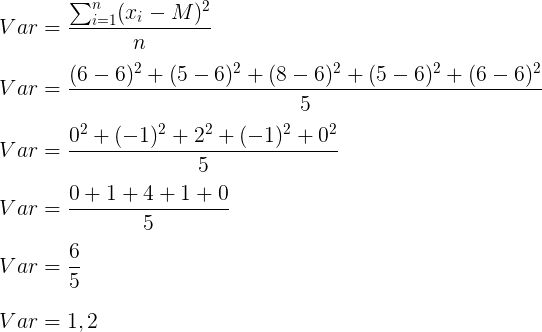
Resposta: B
Exercício 3 (Cesgranrio). Uma amostra aleatória de tamanho 5 é retirada de uma população e observa-se que seus valores, quando postos em ordem crescente, obedecem a uma Progressão Aritmética.
Se a variância amostral não viciada vale 40, qual é o valor da razão da Progressão Aritmética?
a) 3
b) 5√2
c) 4
d) 2√5
e) 1
Resolução
Considerando que a amostra, em ordem crescente, tem a característica de uma P.A., esses 5 números podem ser representados por: x – 2r; x – r; x; x + r; x + 2r, onde r é a razão e x é o elemento central.
Calculando a média aritmética:
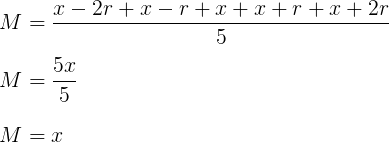
Sabendo que M = x, e que a variância amostral é igual a 40, temos:
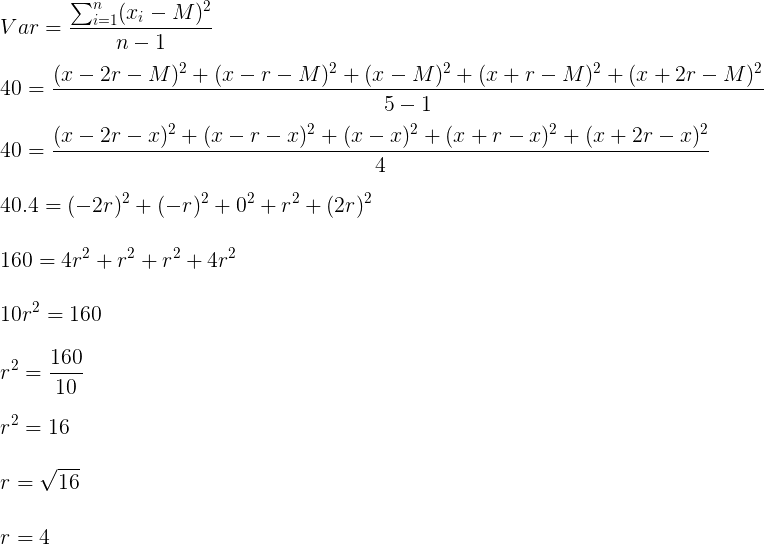
Resposta: C
Exercício 4 (Cetro). Em uma distribuição cujos valores são iguais, o valor do desvio-padrão é:
a) 1.
b) 0.
c) negativo.
d) 0,5.
e) 0,25.
Resolução
Como os valores são iguais, eles também serão iguais à media aritmética.
Analisando as fórmulas de desvio padrão e variância, podemos concluir que a variância será igual a zero, e consequentemente, o desvio padrão também será.
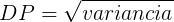
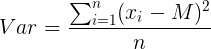
Resposta: B
Gostou dos nossos exercícios sobre variância e desvio padrão?
Deixe o seu comentário.

Na questão 2 há um erro. A fórmula de variância é a soma de todos os elementos (x-média)² sobre (n-1). A resposta correta seria 1,5; não 1,2.
Olá Letícia,
Existem duas fórmulas para o cálculo de variância, uma para a amostral e outra para a populacional.
Por favor, podem me ajudar?
Os preços do pacote de café, pesando 500 g, obtidos em diferentes supermercados
locais, são: R$ 3,50, R$ 2,00, R$ 1,50 e R$ 1,00. Com base nessas informações,
julgue (justificando) os itens que se seguem:
(1) O preço médio do pacote de café de 500 g vale R$ 2,00.
(2) Se todos os preços tiverem uma redução de 50 %, o novo preço médio será de R$
1,50.
(3) A variância dos preços é igual a 0,625.
(4) Se todos os preços tiverem um acréscimo de R$ 1,00, o coeficiente de variação dos
preços não se altera.
(5) Se todos os preços tiverem um acréscimo de R$ 1,00, o coeficiente de variação dos
preços será aproximadamente igual a 31,18 %.
(6) Se todos os preços tiverem um aumento de 50 %, a nova variância será exatamente
igual à anterior, pois a dispersão não será alterada.
(7) A variância ficará multiplicada por 2,25 se todos os preços tiverem um aumento de
50 %.
) Um instituto de pesquisa fez um levantamento dos preços por quilo de vários produtos em um sacolão. Os resultados estão na tabela a seguir. Qual é a Variância e o Desvio Padrão, respectivamente, do preço por quilo dos produtos nesse sacolão? *
2 pontos
R$ 3,20; R$ 3,00
R$ 2,20; R$ 1,80
R$ 1,36; R$ 1,17
R$ 1,50; R$ 1,10
8) A tabela a seguir apresenta uma distribuição de frequência das áreas de 400 lotes. Com referência a esta tabela calcule a Variância e o Desvio Padrão. *
2 pontos
32180,56m2; 134,22m2
36159,75m2; 190,16m2
38225,40m2; 176,25m2
39126,55m2; 180,44m2
Como saber qual termo usar no denominador? (n) ou (n-1)?
Olá Henrique!
Sugiro a você que leia o post abaixo:
https://sabermatematica.com.br/variancia-e-desvio-padrao.html
Por favor como calcular Foi feita uma gincana na Unitins, e a média das foi 10, com variância de 25. Calcule a probabilidade dessa média ser maior que 5 e da média ser menor que 10, ou seja, P(x>5) e P(x< que 10), demonstrando por meio do gráfico