Estudando matemática e estatística para concursos e ENEM? Confira aqui a nossa publicação sobre a variância e o desvio padrão, com definição e exemplos.
Bom estudo!
Variância
A variância é uma medida de dispersão que demonstra a distância de cada dado até o valor central (média aritmética).
Uma variância pequena indica que as amostras estão próximas à média aritmética (valor central), enquanto uma variância elevada indica exatamente o contrário.
Existem dois tipos de variância, a amostral e a populacional. Vejamos cada uma delas e como são calculadas.
- Variância amostral
A variância amostral considera apenas uma amostra e não toda a população, podendo ser calculada através da seguinte fórmula:
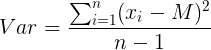
Onde:
Var = variância amostral
n = quantidade de elementos da amostra
M = média aritmética da amostra
xi = cada um dos elementos da amostra
- Variância populacional
A variância populacional, como o próprio nome deixa claro, considera toda a população, e não apenas uma amostra. A fórmula é a seguinte:
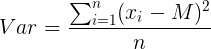
Onde:
Var = variância populacional
n = quantidade de elementos da amostra
M = média aritmética da amostra
xi = cada um dos elementos da amostra
Desvio Padrão
O desvio padrão, por sua vez, indica se o valor da média aritmética é confiável para substituir o conjunto de dados.
A fórmula utilizada para o cálculo do desvio padrão é a seguinte:
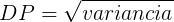
Exemplo 1: As idades de Antonio, Bruno, Carlos e Deco são, respectivamente, 10, 15, 40 e 27 anos. Calcule a variância e o desvio padrão das idades.
- Calculando inicialmente a média aritmética:
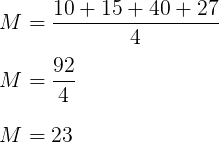
- Calculando a variância populacional, considerando que estamos levando em consideração toda a população analisada:
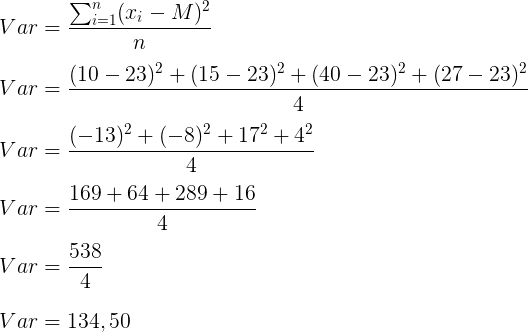
- Calculando o Desvio Padrão:
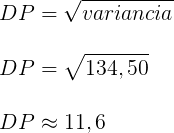
Exemplo 2: Pedro está em dúvida se compra a ação A ou a ação B. A escolha será feita com base na análise da performance dos 5 dias da última semana. Ao levantar o histórico, observou os seguintes rendimentos:
- Ação A
Segunda-feira: -2%
Terça-feira: -1%
Quarta-feira: 3%
Quinta-feira: 8%
Sexta-feira: -3%
- Ação B
Segunda-feira: 0%
Terça-feira: 1%
Quarta-feira: 3%
Quinta-feira: 0%
Sexta-feira: 1%
A primeira análise de Pedro foi calcular a média aritmética dos rendimentos diários de cada ação, onde observou que as médias são exatamente iguais:
- Ação A
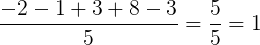
- Ação B
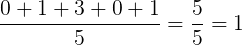
Calculando a variância amostral da ação A:
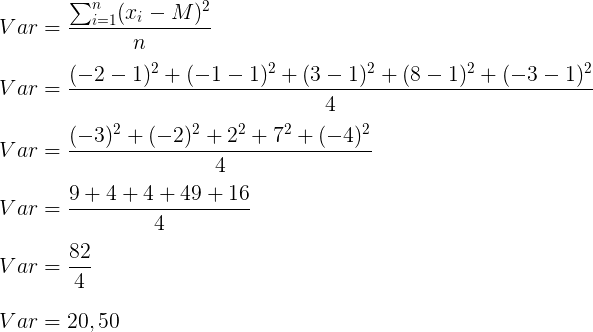
Calculando a variância amostral da ação B:
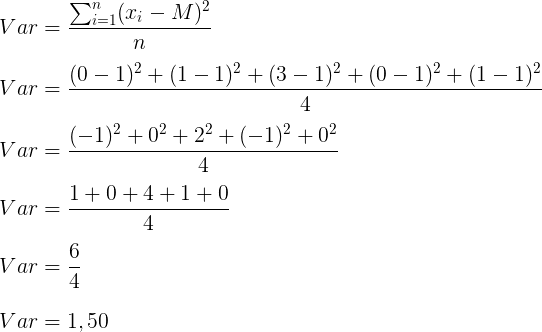
Calculando o Desvio Padrão da ação A:
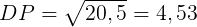
Calculando o Desvio Padrão da ação B:
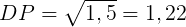
O desvio padrão da ação B é menor que o desvio padrão da ação A. Neste caso, podemos afirmar que a ação B é a que possui maior regularidade, e em nosso caso específico, a que possui o menor risco.
Lembre-se sempre de associar Desvio Padrão a Regularidade.
Gostou da nossa publicação sobre Variância e Desvio Padrão?
Deixe o seu comentário.
