Saber Matemática Matemática: Conteúdo, provas e exercícios resolvidos.
Confira aqui vários exercícios resolvidos sobre o sistema de numeração binário (números binários). Trata-se de um sistema de numeração que utiliza apenas dois algarismos (0 e 1).
Bom estudo!
Questão 1 (FUSAR – UFF). Os computadores utilizam o sistema binário ou de base 2 que é um sistema de numeração em que todas as quantidades se representam com base em dois números, ou seja, (0 e 1). Em um computador o número 2012, em base decimal, será representado, em base binária, por:
A) 110111.
B) 11111011100.
C) 111110111000.
D) 111110111.
E) 1111010101
Resolução
Para transformarmos um número do sistema decimal para o binário é necessário transformá-lo em uma soma de potências de 2. Veja:
2012 = 1024 + 512 + 256 + 128 + 64 + 16 + 8 + 4
2012 = 210 + 29 + 28 + 27 + 26 + 24 + 23 + 22
2012 = 1.210 + 1.29 + 1.28 + 1.27 + 1.26 + 0.25 + 1.24 + 1.23 + 1.22 + 0.2¹ + 0.20
De onde concluímos que o número 2012, representado na base binária será 11111011100.
Resposta: B
Questão 2 (CRF SC – IESES). Abaixo apresentamos quatro números em suas representações binárias.
1) 0101001
2) 1101001
3) 0001101
4) 1010110
Assinale a alternativa que apresenta o somatório dos 4 números acima convertidos para o formato decimal.
a) 245
b) 101
c) 111
d) 267
Resolução
Para resolvermos a questão temos duas opções, somar e depois converter, ou converter e depois somar. Como estamos mais familiarizados a somar números na base decimal, penso que é melhor transformar para a base decimal e depois efetuar a soma. Efetuando as transformações:
1) 0101001
= 0.26 + 1.25 + 0.24 + 1.23 + 0.22 + 0.2¹ + 1.20
= 0 + 32 + 0 + 8 + 0 + 0 + 1
= 41
2) 1101001
= 1.26 + 1.25 + 0.24 + 1.23 + 0.22 + 0.2¹ + 1.20
= 64 + 32 + 0 + 8 + 0 + 0 + 1
= 105
3) 0001101
= 0.26 + 0.25 + 0.24 + 1.23 + 1.22 + 0.2¹ + 1.20
= 0 + 0 + 0 + 8 + 4 + 0 + 1
= 13
4) 1010110
= 1.26 + 0.25 + 1.24 + 0.23 + 1.22 + 1.2¹ + 0.20
= 64 + 0 + 16 + 0 + 4 + 2 + 0
= 86
Total:
41 + 105 + 13 + 86 = 245
Resposta: A
Questão 3 (AOCP – EMPREL). Os números binários são essenciais para a o processamento de dados em um computador. Sabendo disso, assinale a alternativa que apresenta corretamente o resultado da seguinte adição binária:
Adição Binária:
A) 111
B) 1100
C) 1001
D) 101
E) 000
Resolução
A adição binária é muito semelhante a adição no sistema decimal. Devemos apenas observar que, como existem apenas dois algarismos, 1 + 1 = 10.
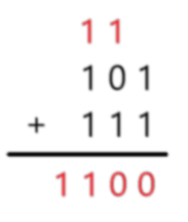
Resposta: B
Questão 4 (Funcab – CBM RO). Observe o número de identificação do armário de um bombeiro, escrito na base 2, ou seja, no sistema binário.
11100110101
Determine o número que representa essa identificação no sistema decimal.
A) 1.792
B) 1.813
C) 1.845
D) 1.850
E) 1.909
Resolução
Faremos a transformação do sistema binário para o decimal utilizando potências de 2:
11100110101(2) = 1.210 + 1.29 + 1.28 + 0.27 + 0.26 + 1.25 + 1.24 + 0.23 + 1.22 + 0.2¹ + 1.20
11100110101(2) = 1.1024 + 1.512 + 1.256 + 0 + 0 + 1.32 + 1.16 + 0.8 + 1.4 + 0 + 1.1
11100110101(2) = 1024 + 512 + 256 + 32 + 16 + 4 + 1
11100110101(2) = 1845(10)
Resposta: C
Gostou dos exercícios resolvidos sobre os números binários?
Deixe o seu comentário.
Adorei para estudar pra prova
obg por dispor da sua atenção nas questões acima
A questão 1 não ta errada não? num era pra ser 1006 ao invés de 1024?
“2012 = 1024 + 512 + 256 + 128 + 64 + 16 + 8 + 4”
Olá Diana,
2.2.2.2.2.2.2.2.2.2 = 1024
deve ser 1006 a depender do metodo no qual vc chegou a resposta eu fiz diferente
2012/2=1006 resto 0
1006/2=503 resto 0
503/2=251 resto 1
251/2=125 resto 1
125/2=62 resto 1
62/2=31 resto 0
31/2=15 resto 1
15/2=7 resto 1
7/2=3 resto 1
3/2=1 resto 1
resposta ent 11111011100 fica a dica
Nesse caso como eu fiz eu acho mais fácil se você não entendeu vc deve saber q se ler de baixo pra cima o certo e da direita pra esquerda só que ai esta um embaixo do outro ent de baixo pra cima e se reparar pelos números no calculo esta 1111011100 e pq no final repare que 3/2=1 esse 1 conta no código binário blz galera espero ter ajudado
porque 2012/2 nao é 1024, é 1006. dããããrrr
Ola João!
Não entendi a sua dúvida.
Mano, o 1024 não a ver com ser 2012/2, tem a ver com ser POTENCIA DE 2, pq faz parte da conversão para binario. dãããrrr 2 elevado na 10 = 1024. dãããrr
olá, joão. Refaça seu calculo , pois se vc multiplicar 1024 x 2 = 2048 e não 2012 . Preste mais atenção , é por um erro básico que vc perde uma questão .
Eu não entendi a questão 01!! De decimal pra binário num divide por 2 até não ter mais restos??
Olá Daniele!
Existem várias formas de se chegar ao mesmo resultado rsrs.
Adorei os exercícios, consegui acertar os dois <3 Se puder postar outros no estilo ENEM eu iria amar
Ameiii os exercícios aceitei todos !!!!
BOA TARDE
NO EXERCÍCIO 1 PQ QUANDO O EXPOENTE 5 O MULTIPLICADOR É ZERO E NÃO 1 COMO OS DEMAIS?
2012 = 1.210 + 1.29 + 1.28 + 1.27 + 1.26 +( 0.25) + 1.24 + 1.23 + 1.22 + 0.2¹ + 0.20
Olá Tales,
Porque não utilizamos o 32 na soma abaixo:
2012 = 1024 + 512 + 256 + 128 + 64 + 16 + 8 + 4