Estudando matemática e estatística para concursos? Confira aqui vários exercícios resolvidos sobre as medidas de dispersão.
Bom estudo!
Exercício 1 (CONSULPLAN). Considerando as medidas de posição e as medidas de dispersão usadas na bioestatística, relacione adequadamente as colunas a seguir.
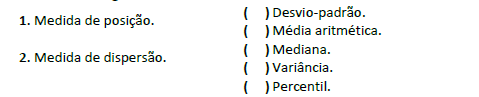
A) 1, 2, 2, 1, 2.
B) 1, 1, 2, 1, 2.
C) 2, 1, 1, 2, 1.
D) 2, 2, 1, 2, 1.
Resolução
As medidas de dispersão apresentadas na segunda coluna são o desvio padrão e a variância.
Para ver todas as medidas de dispersão clique aqui.
Resposta: C
Exercício 2 (IBFC). São consideradas Medidas de Dispersão na análise estatística:
A) A Variância e o Desvio Padrão.
B) A Média, a Moda e a Mediana.
C) A Média, a Variância e o Desvio Padrão.
D) A Moda e a Média.
Resolução
Conforme visto na questão 1, a variância e o desvio padrão são medidas de dispersão.
Média, moda e mediana são consideradas medidas de posição.
Resposta: A
Exercício 3 (IBFC). A alternativa que apresenta uma série de valores cuja dispersão ou variabilidade seja maior é:
A) 33, 33, 33, 33, 33
B) 33, 32, 34, 32, 34
C) 31, 32, 33, 34, 35
D) 30, 35, 35, 33, 32
E) 10, 20, 30, 40, 65
Resolução
Os valores que apresentam maior dispersão ou variabilidade são aqueles que, no geral, possuem elementos mais distantes da média aritmética.
Resposta: E
Exercício 4 (IBFC). Em um hospital foram registrados os “pesos” em Kg, das crianças atendidas, em um mesmo dia, conforme lista abaixo:

O desvio médio referente ao “peso”, em Kg, das crianças atendidas nesse dia no hospital foi de:
A) 0,4
B) 0,4
C) -0,2
D) 0
E) 0,5
Resolução
Calculando a média dos “pesos” das crianças:
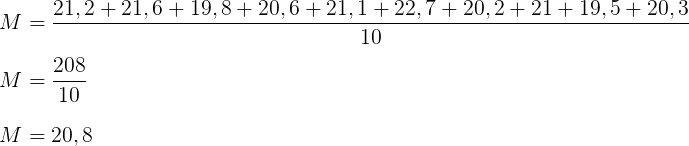
Calculando os desvios:
21,2 – 20,8 = 0,4
21,6 – 20,8 = 0,8
19,8 – 20,8 = -1,0
20,6 – 20,8 = -0,2
21,1 – 20,8 = 0,3
22,7 – 20,8 = 1,9
20,2 – 20,8 = -0,6
21,0 – 20,8 = 0,2
19,5 – 20,8 = -1,3
20,3 – 20,8 = -0,5
Desvio médio:
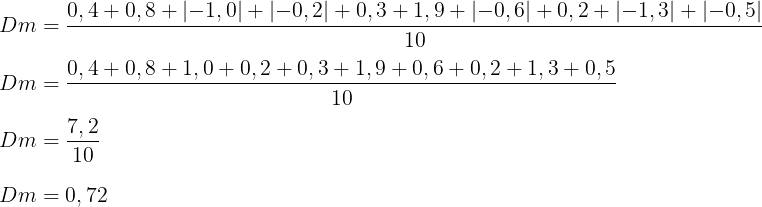
Resposta: D
Gostou dos nossos exercícios resolvidos sobre as medidas de dispersão?
Deixe o seu comentário.
