Confira aqui vários exercícios resolvidos sobre equações logarítmicas, todos retirados de provas de concursos, vestibulares e ENEM.
Bom estudo!
Questão 1 (UP). A solução da equação logarítmica abaixo na variável real x é um número
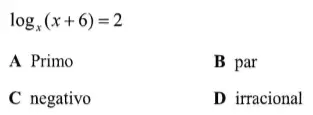
Resolução
Pela definição de logaritmos, temos:
x² = x + 6
x² – x – 6 = 0
Podemos resolver a equação do segundo grau pelo método da soma e produto:
S = -b/a = -(-1)/1 = 1
P = c/a = -6/1 = -6
Os dois números cuja soma é igual a 1 e o produto é igual a -6 são os números -2 e 3.
Como x representa a base do logaritmo, que deve ser maior que zero e diferente de 1, descartamos a solução -2.
Finalizando, 3 é um número primo.
Resposta: A
Questão 2 (UP). A solução da equação logarítmica log10 (x-4) = 2 é:
A) x = 6.
B) x = 10.
C) x = 50.
D) x = 100.
E) x = 104.
Resolução
Pela definição de logaritmos, temos:
10² = x – 4
100 = x – 4
x = 100 + 4
x = 104
Resposta: E
Questão 3 (CETREDE). Pode-se afirmar que o conjunto verdade da equação logarítmica log x + log (x+1) – log 6 = 0 é
A) {3}.
B) {2, –3}.
C) {2}.
D) {–2, 3}.
E) {2, 3}.
Resolução
Aplicando as propriedades de adição e subtração de logaritmos, temos:
log x + log (x+1) – log 6 = 0
log[ x.(x + 1) / 6 ] = 0
Pela definição de logaritmos:
x.(x + 1) / 6 = 100 = 1
x.(x + 1) / 6 = 1
x.(x + 1) = 6
x² + x – 6 = 0
Temos uma equação do segundo grau que pode ser resolvida através do método da soma e do produto:
S = -b/a = -1/1 = -1
P = c/a = -6/1 = -6
Os dois números cuja soma é igual a -1 e o produto é igual a -6 são -3 e 2. Como o logaritmando deve ser maior que zero, descartamos o -3.
Resposta: C
Gostou dos nossos exercícios resolvidos sobre equações logarítmicas?
Deixe o seu comentário.

É a primeira vez que acesso este site, procurando pelo assunto exercícios resolvidos com Logarítmos. Gostei, pena que foram poucos. De qualquer forma, parabéns pelo trabalho, te desejo muito sucesso.
Obrigado José!
Volte sempre.