Procurando exercícios resolvidos sobre inequação do segundo grau? Aqui você encontra uma seleção especial, todos retirados das mais diversas provas de concursos.
As inequações, sobretudo as de segundo grau, aparecem com frequência em provas de concursos e costumam retirar pontos da maioria dos concorrentes.
Bons estudos.
Questão 1 (BNDES – Cesgranrio). O conjunto-solução da inequação 9 – x² > 0 é:
a) – 3 > x > 3
b) – 3 < x < 3
c) x = 3
d) x < 3
e) x > 3
Resolução
Sabemos que a função f(x) = 9 – x² é uma função quadrática, onde a=-1, b=0 e c=9.
Podemos concluir que o gráfico de f é uma parábola com a concavidade para baixo, pois a<0.
Vamos agora descobrir as raízes da função f resolvendo a equação:
9 – x² = 0
x² = 9
x = ± √9
x = ± 3
Daí, o conjunto solução da equação é S = {-3, 3}
Veja como fica o gráfico de f com as informações que descobrimos:
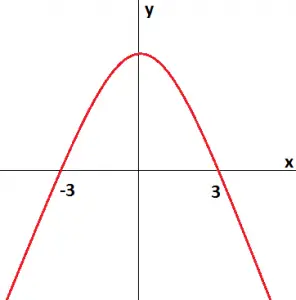
Como queremos os valores de x onde f(x) > 0, temos que o conjunto solução é:
S = {x∈R | -3<x<3 }
Resposta: B
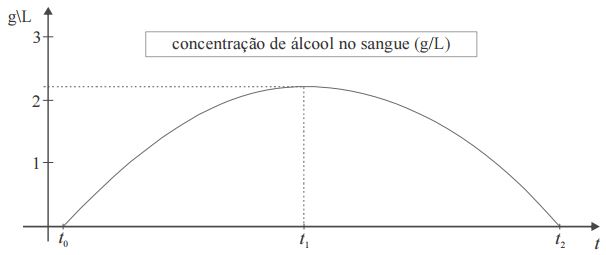
Questão 2 (PRF – Cespe). Considere que o nível de concentração de álcool na corrente sanguínea, em g/L, de uma pessoa, em função do tempo t, em horas, seja expresso por N = – 0,008(t² – 35t + 34). Considere, ainda, que essa pessoa tenha começado a ingerir bebida alcoólica a partir de t = t0 (N(t0 = 0), partindo de um estado de sobriedade, e que tenha parado de ingerir bebida alcoólica em t = t1, voltando a ficar sóbria em t = t2. Considere, por fim, a figura acima, que apresenta o gráfico da função N(t) para t є [t0, t2]. Com base nessas informações e tomando 24,3 como valor aproximado de √589, julgue o item a.
a) O nível de concentração de álcool na corrente sanguínea da pessoa em questão foi superior a 1 g/L por pelo menos 23 horas.
Resolução:
Sendo N = – 0,008(t² – 35t + 34) a função que mede a concentração de álcool em função do tempo, precisamos saber quando N > 1.
Devemos então resolver a inequação do segundo grau:
– 0,008(t² – 35t + 34) > 1
– 8(t² – 35t + 34) > 1000
t² – 35t + 34 > – 125
t² – 35t + 159 > 0
Calculando Δ:
Δ = b² – 4ac
Δ = (-35)² – 4.1.159
Δ = 1225 – 636
Δ = 589
Utilizando a fórmula de Bhaskara:
t = (-b ± √Δ)/2a
t = (-(-35) ± √589)/2.1
t = (35 ± 24,3)/2
Assim,
t’ = (35 + 24,3)/2 = 59,3/2 = 29,65
t” = (35 – 24,3)/2 = 10,7/2 = 5,35
Pelo gráfico da função e analisando as raízes temos que o conjunto solução é:
S = {5,35 ˂ x ˂ 29,65}
E a diferença entre os extremos será 24,3.
Questão CERTA.
Questão 3 (PM Ceará). O batalhão de polícia militar de uma cidade constituída dos bairros B1, B2 e B3 será dividido em três pelotões distintos de modo que cada um fique responsável pelo policiamento ostensivo de um desses bairros. As populações dos bairros B1, B2 e B3 são, respectivamente, iguais a 60.000, 66.000 e 74.000 pessoas; o batalhão possui um efetivo de 4.000 militares dos quais 300 trabalham exclusivamente em uma central única de comunicação e inteligência, não caracterizando atividade policial ostensiva; e todos os militares do batalhão residem na cidade. Com base nessa situação hipotética, julgue a afirmação a seguir:
Se as quantidades de policiais do sexo feminino em cada um dos três pelotões são números que satisfazem à inequação x² – 520x + 64.000 < 0, então, no batalhão, há mais de 600 policiais do sexo feminino.
Resolução:
Primeiramente vamos achar as raízes da equação x² – 520x + 64.000 = 0
Note que a = 1, b = -520, c = 64000
Calculando o valor de Δ:
Δ = b² – 4ac
Δ = (-520)² – 4.1.(64000)
Δ = 270400 – 256000
Δ = 14400
Calculando as raízes:
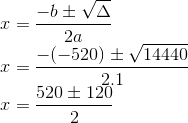
Logo, as duas raízes serão:
x’ = (520 + 120) / 2 = 640/2 = 320
x” = (520 – 120) /2 = 400/2 = 200
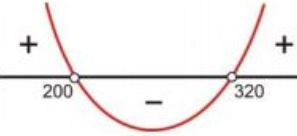
Por se tratar de uma equação do segundo grau com a>0, temos uma parábola com cavidade para cima, cortando o eixo x em 200 e 320. Logo, na inequação x² – 520x + 64.000 < 0, temos que 200 < x < 320.
Disto temos que cada um dos três pelotões tem mais que 200 e menos que 320 mulheres, logo, o batalhão tem mais que 600 mulheres.
Resposta: CERTO
Questão 4 (BB – Cesgranrio). A proposição funcional “Para todo e qualquer valor de n, tem-se 6n < n² + 8 ” será verdadeira, se n for um número real
(A) menor que 8.
(B) menor que 4.
(C) menor que 2.
(D) maior que 2.
(E) maior que 3.
Resolução:
Vamos resolver a inequação: n² – 6n + 8 > 0, para isto, devemos achar as raízes da equação n² – 6n + 8 = 0:
Pelo método de soma e produto:
Soma = -b/a = 6/1 = 6
Produto = c/a = 8/1 = 8
Os dois números cuja soma é 6 e o produto é 8 só podem ser 2 e 4.
Veja em nosso material didático que o gráfico de uma função do segundo grau é uma parábola, e que quando a > 0 a parábola tem a concavidade para cima. Logo, a proposição é verdadeira para n<2 ou n>4.
Resposta: C
Questão 5 (RFB – Esaf). Considere as inequações dadas por:
f(x) = x² – 2x + 1 ≤ 0
g(x) = -2x² + 3x + 2 ≥ 0
Sabendo-se que A é o conjunto solução de f(x) e B o conjunto solução de g(x), então o conjunto Y = A ∩ B é igual a:
a) Y = { x ∈ R | -1/2 < x ≤ 2 }
b) Y = { x ∈ R | -1/2 ≤ x ≤ 2 }
c) Y = { x ∈ R | x = 1 }
d) Y = { x ∈ R | x ≥ 0 }
e) Y = { x ∈ R | x ≤ 0 }
Resolução
Vamos calcular as raízes de f(x):
Δ = b² – 4.a.c = (-2)² – 4.1.1 = 4 – 4 = 0
x = (-b +- √Δ)/2a = (2 +- 0)/2 = 2/2 = 1
Como o gráfico de uma função do segundo grau é uma parábola, f(x) só tem uma raíz igual a 1 e a>0, temos uma parábola com o “buraco” para cima e o vértice no ponto (1,0).
Logo, f(x) é menor ou igual a zero apenas quando x=1.
Logo A = {1}.
Como não temos a opção de Y ser vazio, só nos resta a alternativa C.
Questão 6 (BASA – Cesgranrio). No conjunto dos números reais, considere as seguintes duas inequações:
Inequação 1: 5x – 7 > x² – x + 1
Inequação 2: x + 6 > -x + 10
Um número real x, que é solução da inequação 2, também será solução da inequação 1, se, e somente se, for solução da inequação
(A) x² – 16 > 0
(B) 1/x < 1/4
(C) -x < -4
(D) 4x – 16 < 0
(E) x + 1 > x + 9
Resolução
Resolvendo a primeira inequação:
5x – 7 > x² – x + 1
x² – x + 1 – 5x + 7 < 0
x² – 6x + 8 < 0
Utilizaremos agora o método da soma e do produto para encontrarmos as raízes da equação x² – 6x + 8 = 0.
S = -b/a = -(-6)/1 = 6
P = c/a = 8/1 = 8
Os dois valores cuja soma é igual a 6 e o produto é igual a 8 são 2 e 4.
O gráfico da função x² – 6x + 8 é uma parábola com concavidade para cima. Ela será negativa apenas no intervalo ]2, 4[.
Resolvendo a segunda inequação:
x + 6 > -x + 10
2x – 4 > 0
x > 2
Analisando os valores de x que atendem a inequação 2, eles também atenderão a inequação 1 se forem menores que 4, ou seja, x < 4, que é equivalente a inequação:
4x – 16 < 0
Resposta: D
Questão 7 (PM ES – AOCP). Resolvendo-se a inequação do segundo grau 2x² + 13x – 7 < 0, no conjunto dos números reais (R), obtém-se o conjunto solução S igual a
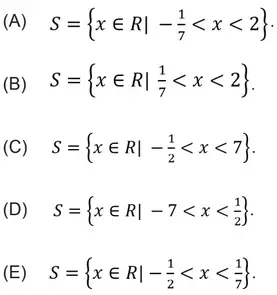
Resolução
Temos uma inequação do segundo grau. A maneira mais fácil de analisar uma equação deste tipo é analisando a função do segundo grau:
f(x) = 2x² + 13x – 7
Onde:
a = 2
b = 13
c = -7
Observe que o gráfico da função é uma parábola côncava para cima, ou seja, os valores de x que fazem f(x)<0 são aqueles que estão entre as raízes da função.
Utilizaremos a fórmula de Bháskara para o cálculo das raízes:
Δ = b² – 4ac
Δ = 13² – 4.2.(-7)
Δ = 169 + 56
Δ = 225
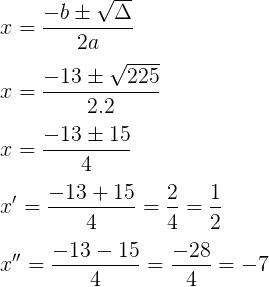
S = {x∈R | -7 < x < 1/2}
Resposta: D
Gostou dos exercícios resolvidos sobre as inequações do segundo grau?
Deixe o seu comentário.
Quero ter aceso das aulas