Procurando exercícios resolvidos sobre o diagrama de ramos e folhas? Confira aqui várias questões comentadas, todas retiradas dos últimos concursos públicos.

Não deixe de acessar também os nossos conteúdos sobre outros tópicos da matemática e estatística.

Bom estudo!

 

 

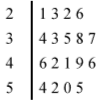
Questão 1 (ABIN – CESPE 2010). Considerando que o diagrama de ramos e folhas acima mostra a distribuição das idades (em anos) dos servidores de determinada repartição pública, julgue os itens subsequentes.

 

a) O primeiro quartil e o terceiro quartil são, respectivamente, 34 e 46 anos de idade.

 

Resolução

Temos aqui um diagrama de ramos e folhas onde os ramos representam as dezenas e as folhas representam as unidades das idades dos servidores.

 

As idades, em ordem crescente, são:

21, 22, 23, 26, 33, 34, 35, 37, 38, 41, 42, 46, 46, 49, 50, 52, 54, 55

 

Os quartis Q₁, Q₂ e Q₃ dividem os valores em quatro partes iguais:

Q₁ = 33

Q₂ = (38 + 41) / 2 = 39,5

Q₃ = 49

Resposta: Errado

 

 

b) A mediana das idades dos servidores é igual a 39,5 anos.

 

Resolução

A mediana é exatamente o valor do meio, quando todos os valores estão em ordem alfabética, ou a média dos dois valores do meio, quando a quantidade de termos é par.

Veja que a mediana já foi calculada é igual a Q₂ = 39,5 anos.

Resposta: Certo

 

 

Questão 2 (TJ AP – FCC 2009). O diagrama de ramo e folhas a seguir corresponde às idades dos 40 funcionários de um setor de um órgão público em uma determinada data.

A soma da mediana e da moda destas idades é igual a

a) 67,0

b) 66,5

c) 66,0

d) 65,5

e) 65,0

Resolução

Veja que o os ramos representam as dezenas e as folhas representam as unidades das idades dos 40 funcionários.

 

A mediana é o termo central. Como existem 40 idades, ela será a média dos 20º e 21º termos:

(34 + 34) / 2 = 34

A moda é a idade que aparece com maior frequência. Temos 4 funcionários com 33 anos.

 

Somando a mediana com a moda:

34 + 33 = 67

Resposta: A

 

 

Questão 3 (TRE PI – FCC 2009). O diagrama de ramo e folhas abaixo corresponde às observações das idades de 50 eleitores escolhidos aleatoriamente em uma determinada zona eleitoral:

O valor do módulo da diferença entre a mediana e a moda destas idades observadas é

A) 0

B) 3

C) 10

D) 14

E) 16

 

Resolução

Temos um diagrama de ramos e folhas que representa a idade de 50 pessoas.

Dispostas em ordem crescente, a mediana das idades é a média dos 25º e 26º termos:

(32 + 32) / 2 = 32

A moda é a idade que aparece com maior frequência. Temos 4 eleitores com 46 anos.

 

Calculando o módulo da diferença (o maior pelo menor):

46 – 32 = 14

Resposta: D

 

 

Gostou dos nossos exercícios resolvidos sobre o diagrama de ramos e folhas?

Deixe o seu comentário.