Confira aqui vários exercícios resolvidos sobre os arranjos simples, todos retirados das últimas provas de concursos que cobram análise combinatória.
O ideal é que o aluno já tenha estudado o conteúdo sobre o assunto e também sobre fatorial de um número natural.
Bom estudo!
Questão 1 (BRDE – AOCP 2012). A expressão arranjo é
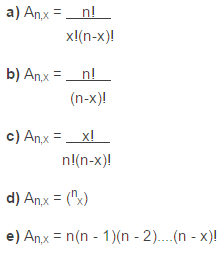
Resolução
Clique aqui para ver que a fórmula utilizada em nosso material didático foi:
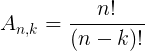
A única diferença para a fórmula da letra B é que foi utilizado o x no lugar do k, o que não faz diferença alguma.
Resposta: B
Questão 2 (PM SC – Cesiep 2011). Em uma corrida com 10 atletas competindo pergunta-se: de quantos modos distintos (combinações) podem ser conquistadas as medalhas de Ouro, Prata e Bronze?
a) 800
b) 1000
c) 720
d) 300
Resolução
Considerando que a ordem importa, temos um arranjo simples com 10 atletas, tomados 3 a 3:
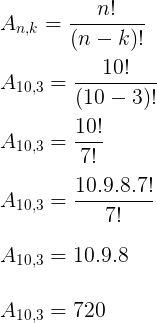
Resposta: C
Questão 3 (Liquigás – CESGRANRIO 2012). Em uma pequena sala de projeção, há cinco cadeiras dispostas em linha, lado a lado, e numeradas de 1 a 5.

Quatro pessoas vão ocupar quatro dessas cadeiras. As possíveis ocupações das cadeiras distinguem-se não só pela cadeira vazia, mas, também, pela disposição das pessoas nas cadeiras ocupadas.
De quantos modos as cadeiras podem ser ocupadas pelas quatro pessoas?
a) 5
b) 20
c) 24
d) 120
e) 1.024
Resolução
Podemos analisar a questão como um arranjo simples explorando a ideia de que 4 cadeiras em 5 serão escolhidas, e que a ordem em cada uma delas é importante.
Temos assim um arranjo de 5 cadeiras, tomadas 4 a 4.
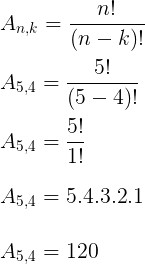
Resposta: D
Questão 4 (Sefaz RJ – Coperj 2010). Em uma fila do cinema há 5 cadeiras consecutivas vazias.
O número de maneiras que três pessoas, A, B e C, podem sentar- se nelas é:
a) 10
b) 15
c) 30
d) 45
e) 60
Resolução
Claramente temos um arranjo de 5 cadeiras, tomadas 3 a 3.
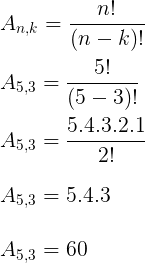
Resposta: E

mucha gracia ,faltou letra por que o meu teclado etá quebrado
Foi bom ter partilhado esta pagina, gostei me ajjude a perceber a ter o dominio de analise combinatoria
muito bom! conseguir acertar todas. é um assunto que cai bastante no concurso que irei prestar.
Posso estar equivocado; mas creio que se o exercício de número 2 – Em uma corrida com 10 atletas competindo pergunta-se: de quantos modos distintos (combinações) podem ser conquistadas as medalhas de Ouro, Prata e Bronze? trata-se de uma combinação então o resultado teria que ser 120, porque se não estaríamos falando de arranjo.
Olá José!
A “combinação” citada no enunciado deve ser interpretada de acordo com o seu significado no dicionário:
1. ato ou efeito de combinar.
2. reunião de coisas, semelhantes ou diferentes, em determinada ordem.
Cabe a nós interpretar se 10 atletas, tomados 3 a 3, onde a ordem é relevante, é um arranjo ou uma combinação, no contexto da análise combinatória.
Esta questão é um arranjo pois a ordem importa , é diferente vc ganhar a medalha de ouro e a de bronze.É diferente ser campeão e 3° colocado .
muito obrigado por disponibilizar esse conteúdo de forma tão explicativa, me ajudou muito, já tinha estudado o conteúdo, porém essas suas resoluções solidificaram melhor o conteúdo, pois ainda tinha algumas dúvidas quanto ao uso de cada uma, obrigado.
Prezado Professor
Há dois dias, em situação de prova, deparei-me com a seguinte questão:
* Em um quadro para chaves, há uma fileira de 6 ganchos vazios.
Três chaves distintas devem ser posicionadas nessa fileira, sendo uma em cada gancho, de modo que entre duas chaves imediatamente próximas sempre tenha exatamente um gancho vazio. O número de maneiras diferentes de se posicionarem as chaves nessa fileira de ganchos é? *
Bem, Professor, em prova às vezes um e outro detalhes podem passar despercebidos, mas a condicional ENTRE DUAS CHAVES IMEDIATAMENTE PRÓXIMAS SEMPRE TENHA EXATAMENTE UM GANCHO VAZIO parece ser um restritivo impróprio para o resultado informado como correto, que foi 12 (doze maneiras).
Peço ao professor, dentro das possibilidades, a análise do problema anotado.
Muito obrigado!
Inicialmente podemos colocar 3,0,2,0,1,0= 6 ou 0,3,0,2,0,1,0 =6
6 + 6=12
Essa foi a minha lógica. Acho que por isso chegamos ao resultado 12
Espero ter ajudado
Não entendi como chegou aos números 3,0,2,0,1,0 & 0,3,0,2,0,1,6, poderia explicar melhor como chegou nesta conclusão?
3 chaves para escolher uma e colocar no primeiro gancho. um gancho vazio e duas chaves para escolher uma para colocar no gancho novamente pula um gancho e coloca a ultima chave e depois s´inverteu o processo.
Um time de de salão de futebol possui 10 atletas mas somente 5entraram para jogar.calcule os arranjos possíveis
obrigado!!!!!!!!!!!!