Procurando exercícios resolvidos sobre polinômios? Chegou ao site certo.
Aqui a matemática é abordada de forma simples e objetiva.
Confira uma seleção de questões resolvidas retiradas de vários concursos pelo país.
Bom estudo!
Questão 1 (Guarda Civil SP). O resto da divisão do polinômio x³ + 3x² – 5x + 1 por (x-2) é:
a) 1
b) 2
c) 10
d) 11
e) 12
Resolução:
Como a divisão gerou algumas dúvidas nos comentários, a dica é tirar a prova real:
(x – 2).(x² + 5x + 5) + 11
x³ + 5x² + 5x – 2x² – 10x – 10 + 11
x³ + 3x² – 5x + 1
Resposta: D
Questão 2 (Guarda Civil SP). Considere o polinômio:
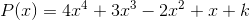
Sabendo que P(1) = 2, então o valor de P(3) é:
a) 386.
b) 405.
c) 324.
d) 81.
e) 368.
Resolução:
Como P(1) = 2:
P(1) = 4.1 + 3.1 – 2.1 + 1 + k = 2
4 + 3 – 2 + 1 + k = 2
6 + k = 2
k = 2 – 6
k = – 4
O polinômio será P(x) = 4x4 + 3x³ – 2x² + x – 4
Calculando P(3):
P(x) = 4x4 + 3x³ – 2x² + x – 4
P(3) = 4.34 + 3.3³ – 2.3² + 3 – 4
P(3) = 4.81 + 3.27 – 2.9 + 3 – 4
P(3) = 324 + 81 – 18 + 3 – 4
P(3) = 386
Resposta: A
Questão 3 (RFB 2009 – Esaf). Se um polinômio f for divisível separadamente por (x – a) e (x – b) com a ≠ b, então f é divisível pelo produto entre (x–a) e (x–b). Sabendo-se que 5 e -2 são os restos da divisão de um polinômio f por (x – 1) e (x + 3), respectivamente, então o resto da divisão desse polinômio pelo produto dado por (x – 1) e (x + 3) é igual a:
a) 13x/4 + 7/4
b) 7x/4 – 13/4
c) 7x/4 + 13/4
d) -13x/4 – 13/4
e) -13x/4 – 7/4
Resolução:
Primeiramente, o resto da divisão de um polinômio P(x) por (x-a) é igual a P(a).
Dividindo o polinômio f pelo polinômio de grau 2, resultado do produto (x-1).(x+3). Observe que o resto deve ter grau 1 ou 0 (se divisão exata).Vamos chamar o resto de ax + b.
Temos::
P(1) = 5 (5 é o resto da divisão de f por x-1)
P(-3) = -2 (-2 é o resto da divisão de f por x+3)
Daí,
a.1 + b = 5
a.(-3) + b = -2
Subtraindo a equação 1 pela equação 2, temos:
4a = 7
a = 7/4
Substituindo “a” na equação 1, temos:
7/4 + b = 5
b = 5 – 7/4
b = 13/4
Concluímos que o resto é ax + b = (7/4).x + 13/4
Resposta: C
Questão 4 (IFB – 2017). Em relação à função f(x) = x5 + 4x³ + 2x + 3 pode-se afirmar:
a) não tem raízes reais.
b) tem cinco raízes reais.
c) tem três raízes reais e duas complexas.
d) tem uma raiz real e quatro complexas.
e) tem duas raízes reais e três complexas.
Resolução
Podemos descartar as opções abaixo:
a) Como a função polinomial é contínua, f(-1) = -4 < 0, e f(0) = 3 > 0, podemos concluir que existe uma raiz real no intervalo [-1, 0].
f(-1) = (-1)5 + 4.(-1)³ + 2.(-1) + 3
f(-1) = -1 -4 – 2 + 3
f(-1) = -4
f(0) = 05 + 4.0³ + 2.0 + 3
f(0) = 3
b) e c) Analisando a derivada f'(x)=5x⁴+12x²+2, temos uma função positiva para todo valor de x. Recapitulando, f'(x) > 0 indica que a função f é crescente. De onde concluímos que a raiz “descoberta” ao analisar a letra a é única. Veja um esboço do gráfico:
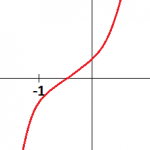
e) Pelo teorema da raiz complexa conjugada, as raízes complexas aparecem aos pares, não sendo possível existirem três.
Resposta: D
Questão 5 (Prefeitura de Terra de Areia RS – Objetiva). Assinalar a alternativa que apresenta o resultado do polinômio abaixo:
2x(5x + 7y) + 9x(2y)
a) 10x + 14xy + 18yx
b) 6x² + 21xy
c) 10x² + 32xy
d) 10x² + 9y
e) 22x + 9y
Resolução
2x(5x + 7y) + 9x(2y)
2x.5x + 2x.7y + 9x.2y
10x² + 14xy + 18xy
10x² + 32xy
Resposta: C
Questão 6 (UP). Sabe-se que o resto da divisão de um polinômio P(x) por binômio do tipo (x – a) é P(a). Qual é o resto da divisão de P(x) = 5x³ – 5x² + 5 por (x + 1)?
A) -1
B) 5
C) 1
D) -5
Resolução
Observe que o binômio (x + 1) possui a = -1.
Calculando o valor de P(a):
P(x) = 5x³ – 5x² + 5
P(-1) = 5(-1)³ – 5(-1)² + 5
P(-1) = 5.(-1) – 5.1 + 5
P(-1) = -5 – 5 + 5
P(-1) = -5
Resposta: D
Questão 7 (PM AL – CESPE). O resto da divisão do polinômio p(x) = 4x³ – 2x² – 3 pelo polinômio q(x) = 2x² – 1 é r(x) = 3x – 3.
Resolução
Efetuando a divisão de polinômios, temos que:
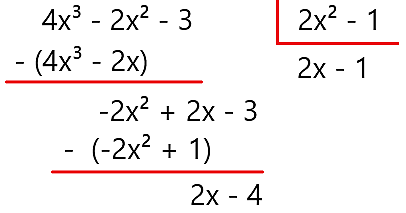
Resposta: ERRADO
Gostou dos nossos exercícios resolvidos sobre os polinômios?
Curta e compartilhe nas redes sociais.

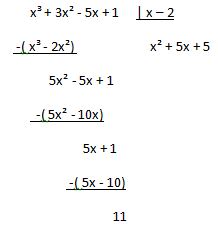
muito bom , só nao entendi a divisão
Eu tbm na entendi o meu deu 2X elevado ao quadrado – 4X + 2
Cara ele errou nos sinais pode confirir um sinal errado da problema onde tem ai +3x ao quadrado sobre -2x ta errado pq era para ser assim o +3x ao quadrado + 2x ao quadrado dá exatamente 5x ao quadrado
Hugo, a divisão de polinômios não é simples. Costuma gerar muitas dúvidas. Fiz uma alteração, acrescentando a prova real.
eu estou a fazer engenharia civil e gostei do vosso blog e espero nela ter um grande apoio para a minha formacao.
Valeu ;)))
obrigada !!
32. como desenvolver em produto de factores lineares o polinómio z evado 2n e -1
Olá, estou na dúvida sobre a questão 1. A resolução não daria resto 9?
Na verdade questão 1. Não daria resto – 9?
1 – (-10) = 1 + 10 = 11
Carine,
Como você concluiu que o resto é 9?
não pois o resultado n é esse
Qual é a sua dúvida Patrick?
Olá Everton,
Havia um pequeno erro de digitação que foi corrigido.
Obrigado.
Patrick Ernany cara acho que ele errou pq 4*1+3*1-2*1+1 ai é para da isso aqui +7-1+k=2 fazendo o calculo vai da -6+k=2 que da k= -6+2 então k= -4 confira ai
Eu estou cm muita dificuldade em resolver polinomios o senhor pode me ajudar indicando sites
desde ja agradeço
Olá Julia!
Entre na página https://sabermatematica.com.br/material-didatico.
Não entendi a questão 1, fiz pelo teorema do resto igualando o divisor a zero e achando a raiz e colocando no dividendo o resultado foi igual a 9, em contrapartida fazendo a divisão normal da 11.
׳+4ײ-3×+5 por ×-2
como a questao 1 da 11 a minha deu 3 enves de somar nao deveria subtrair ess 3xao quadrado por 2x aoo quadrado ? nao entendi pq vc somou
Coloque umas questões mais difíceis prof, por favor.