Vamos falar um pouco sobre as razões trigonométricas no triângulo retângulo. Os temidos seno, cosseno e tangente, tópico básico da trigonometria e um verdadeiro terror na vida da maioria dos estudantes.
Vale ressaltar que a trigonometria é uma das matérias mais importantes da matemática e que contém várias aplicações na Física, na Engenharia, na Cartografia, etc, etc, etc…
Bom estudo a todos.
INTRODUÇÃO
Conforme já comentado, vamos falar um pouco sobre a trigonometria nos triângulos retângulos, onde o estudo está baseado em três relações fundamentais, o seno, o cosseno e a tangente, que são chamadas de razões trigonométricas.
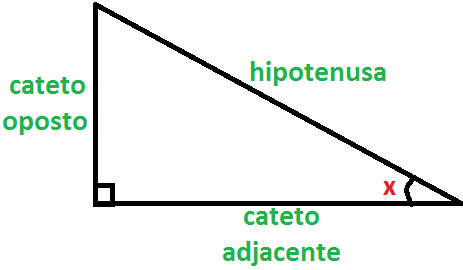
Relembrando, em um triângulo retângulo, chamamos de hipotenusa o lado oposto ao ângulo reto e de cateto os demais lados. Veja a figura:
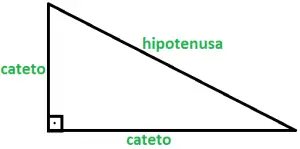
Vamos falar sobre cada um deles.
SENO
Em um triângulo retângulo, chamamos de seno de um ângulo agudo o quociente (razão) entre o cateto oposto a esse ângulo e a hipotenusa.
Veja a figura:
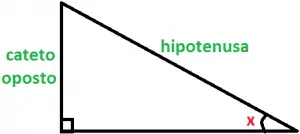
Neste caso,
![]()
COSSENO
Em um triângulo retângulo, chamamos de cosseno de um ângulo agudo o quociente (razão) entre o cateto adjacente a esse ângulo e a hipotenusa.
Veja a figura:
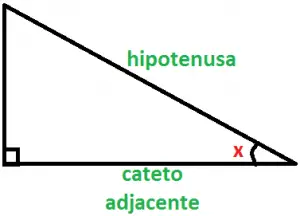
Neste caso,
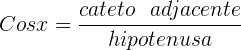
TANGENTE
Em um triângulo retângulo, chamamos de tangente de um ângulo agudo o quociente (razão) entre o cateto oposto e o cateto adjacente a esse ângulo.
Veja a figura:
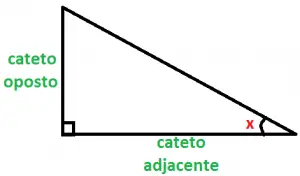
Neste caso,
![]()
ÂNGULOS NOTÁVEIS
No estudo das razões trigonométricas no triângulo retângulo, existem 3 ângulos que são considerados os mais importantes devido a algumas particularidades interessantes e também por serem os mais famosos. Para facilitar a compreensão e a memorização, vamos apresentar o valor do seno, cosseno e tangente desses ângulos em forma de tabela:

COMO CALCULAR
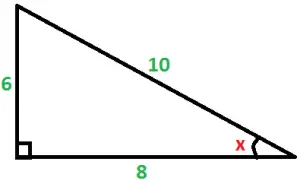
Exemplo 1. Calcular o seno, o cosseno e a tangente de um ângulo x, observando as medidas do triângulo retângulo abaixo:

Exemplo 2. Calcular o valor de k no triângulo retângulo abaixo:
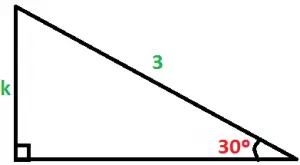
Observe que o exemplo informa que um dos ângulos é 30º. Pela tabela dos ângulos notáveis, sabemos o valor do seno, do cosseno e da tangente de 30º.
E agora? Qual fórmula devemos utilizar?
Basta analisarmos o triângulo. Já sabemos a medida da hipotenusa e queremos saber a medida do cateto oposto. É óbvio que o caminho mais fácil a seguirmos é utilizando a fórmula do seno:
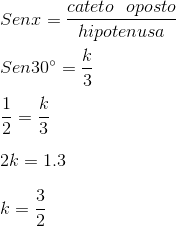
Boa tarde.
Quero receber exercícios de Matematica Ensino Fundamental e Médio
Olá Luciana!
Todo o conteúdo está localizado em nosso menu principal.
Sugiro que inscreva o seu e-mail para receber atualizações.
Como posso calcular o seno de um ângulo alfa?
Olá Higor!
No triângulo retângulo, basta dividir o cateto oposto pela hipotenusa.