Estudando lógica para concursos? Confira aqui uma seleção super especial de exercícios resolvidos sobre proposições lógicas, todos retirados de diversos concursos públicos.

Não deixe de ver na sessão Exercícios Resolvidos outras questões sobre o assunto.

Bons estudos.

Questão 1 (TRT ES – Cespe). Considerando a proposição P: “Se nesse jogo não há juiz, não há jogada fora da lei”, julgue os itens A, B e C seguintes, acerca da lógica sentencial.

Resolução

Consideraremos que:

P = ~Q → ~R

onde,

Q: Nesse jogo há juiz

R: Há jogada fora da lei

A) A negação da proposição P pode ser expressa por “Se nesse jogo há juiz, então há jogada fora da lei”.

Resolução:

Para resolvermos a questão, basta sabermos que a negação de (A → B) é (~B → ~A)

Temos que ~(~Q → ~R) é equivalente a R → Q (Há jogada fora da lei então há juiz)

ERRADO

B) A proposição P é equivalente a “Se há jogada fora da lei, então nesse jogo há juiz”.

Pela questão anterior, A → B e ~B → ~A são equivalentes.

CORRETO

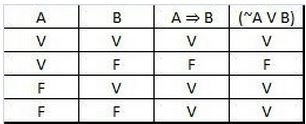
C) A proposição P é equivalente a “Nesse jogo há juiz ou não há jogada fora da lei”.

Veja em nosso conteúdo que A → B e ~A V B são equivalentes

CORRETO

Questão 2 (PF – Cespe). Um jovem, ao ser flagrado no aeroporto portando certa quantidade de entorpecentes, argumentou com os policiais conforme o esquema a seguir:

Premissa 1: Eu não sou traficante, eu sou usuário;

Premissa 2: Se eu fosse traficante, estaria levando uma grande quantidade de droga e a teria escondido;

Premissa 3: Como sou usuário e não levo uma grande quantidade, não escondi a droga.

Conclusão: Se eu estivesse levando uma grande quantidade, não seria usuário.

Considerando a situação hipotética apresentada acima, julgue os itens a seguir.

A) A proposição correspondente à negação da premissa 2 é logicamente equivalente a “Como eu não sou traficante, não estou levando uma grande quantidade de droga ou não a escondi”.

Resolução:

Considerando:

A = Eu sou traficante

B = Levo grande quantidade de drogas

C = Escondi a droga

Temos pela premissa 2:

A  ⇒ B ∧C

Como:

~(P⇒Q) = ~Q⇒~P (negação de uma implicação)

~(P∧Q) = ~P V ~Q

Temos:

~(A  ⇒ B ∧C)  =  ~B V ~C ⇒ ~A

Ou seja, “Como não estou levando uma grande quantidade de droga ou não a escondi, não sou traficante”

Resposta: Errado

B) Se a proposição “Eu não sou traficante” for verdadeira, então a premissa 2 será uma proposição verdadeira, independentemente dos valores lógicos das demais proposições que a compõem.

Resolução:

A premissa 2 tem a estrutura condicional (p⇒q).

Conforme a tabela verdade de p⇒q temos que: Se p é falsa, a proposição condicional será verdadeira, sendo q falsa ou verdadeira.

Resposta: Certo

C) Sob o ponto de vista lógico, a argumentação do jovem constitui argumentação válida.

Observe que é possível que as premissas sejam verdadeiras e a conclusão falsa. Por exemplo:

“Levo uma quantidade grande de droga” é verdadeira.

“Sou usuário” é verdadeira.

“Não sou traficante” é verdadeira.

O argumento seria:

Premissa 1: (V ˄ V) é verdadeira.

Premissa 2: [F  –> (V ˄ ?)] é verdadeira.

Premissa 3: (F ˄ F)  –>?) é verdadeira.

Conclusão: (V –> F) é falsa.

Portanto é um argumento não-válido.

Resposta: Errado

D) Se P e Q representam, respectivamente, as proposições “Eu não sou traficante” e “Eu sou usuário”, então a premissa 1 estará corretamente representada por P∧Q.

Resolução:

Premissa 1: Eu não sou traficante ˄ Eu sou usuário) é equivalente a (p ˄ q).

Resposta: Certo

Questão 3 (BB – FCC). Um jornal publicou a seguinte manchete:

“Toda Agência do Banco do Brasil tem déficit de funcionários.”

Diante de tal inverdade, o jornal se viu obrigado a retratar-se, publicando uma negação de tal manchete. Das sentenças seguintes, aquela que expressaria de maneira correta a negação da manchete publicada é:

(A)  Qualquer Agência do Banco do Brasil não têm déficit de funcionários.

(B)  Nenhuma Agência do Banco do Brasil tem déficit de funcionários.

(C)  Alguma Agência do Banco do Brasil não tem déficit de funcionários.

(D)  Existem Agências com deficit de funcionários que não pertencem ao Banco do Brasil.

(E)  O quadro de funcionários do Banco do Brasil está completo.

Resolução:

Para negar a manchete, basta encontrarmos uma agência que não tem déficit de funcionários.

Letra C.

Questão 4 (BB – Cesgranrio). Qual a negação da proposição “Algum funcionário da agência P do Banco do Brasil tem menos de 20 anos”?

(A) Todo funcionário da agência P do Banco do Brasil tem menos de 20 anos.

(B) Não existe funcionário da agência P do Banco do Brasil com 20 anos.

(C) Algum funcionário da agência P do Banco do Brasil tem mais de 20 anos.

(D) Nenhum funcionário da agência P do Banco do Brasil tem menos de 20 anos.

(E) Nem todo funcionário da agência P do Banco do Brasil tem menos de 20 anos.

Resolução:

Dizer que algum funcionário tem menos de 20 anos significa que pelo menos um funcionário tem menos de 20 anos.

A negação desta afirmação é dizer que nenhum funcionário está nesta condição, ou seja, “nenhum funcionário da agência P do BB tem menos 20 anos”.

A negação de “algum” é “nenhum”.

Resposta: D

Questão 5 (BB – Cesgranrio). A proposição funcional “Para todo e qualquer valor de n, tem-se 6n < n² + 8  ” será verdadeira, se n for um número real

(A) menor que 8.

(B) menor que 4.

(C) menor que 2.

(D) maior que 2.

(E) maior que 3.

Resolução:

Vamos resolver a inequação: n² – 6n + 8 > 0, para isto, devemos achar as raízes da equação n² – 6n + 8 = 0:

Pelo método de soma e produto:

Soma = -b/a = 6/1 = 6

Produto = c/a = 8/1 = 8

Os dois números cuja soma é 6 e o produto é 8 só podem ser 2 e 4.

Veja em nosso material didático que o gráfico de uma função do segundo grau é uma parábola, e que quando a > 0 a parábola tem a concavidade para cima. Logo, a proposição é verdadeira para n<2 ou n>4.

Resposta: C

Questão 6 (TRT – CESPE). Proposições são frases que podem ser julgadas como verdadeiras — V — ou falsas — F —, mas não como V e F simultaneamente. As proposições simples são aquelas que não contêm nenhuma outra proposição como parte delas. As proposições compostas são construídas a partir de outras proposições, usando-se símbolos lógicos, parênteses e colchetes para que se evitem ambiguidades. As proposições são usualmente simbolizadas por letras maiúsculas do alfabeto: A, B, C etc. Uma proposição composta da forma A V B, chamada disjunção, deve ser lida como “A ou B” e tem o valor lógico F, se A e B são F, e V, nos demais casos. Uma proposição composta da forma A ∧ B, chamada conjunção, deve ser lida como “A e B” e tem valor lógico V, se A e B são V, e F, nos demais casos. Além disso, ¬A, que simboliza a negação da proposição A, é V, se A for F, e F, se A for V.

Avalie as afirmações de A a E em verdadeiro ou falso.

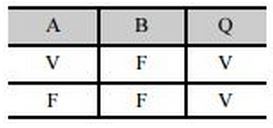
A) Considere que uma proposição Q seja composta apenas das proposições simples A e B e cujos valores lógicos V ocorram somente nos casos apresentados na tabela abaixo.

Nessa situação, uma forma simbólica correta para Q é [A ∧ (¬B)] V [(¬A) ∧ (¬B)].

Resolução

Avaliaremos as quatro opções:

A = V e B = V

[A ∧ (¬B)] V [(¬A) ∧ (¬B)] = [V ∧ (¬V)] V [(¬V) ∧ (¬V)] = [V ∧ F] V [F ∧ F] = F v F = F

A = V e B = F

[A ∧ (¬B)] V [(¬A) ∧ (¬B)] = [V ∧ (¬F)] V [(¬V) ∧ (¬F)] = [V ∧ V] V [F ∧ V] = V v F = V

A = F e B = V

[A ∧ (¬B)] V [(¬A) ∧ (¬B)] = [F ∧ (¬V)] V [(¬F) ∧ (¬V)] = [F ∧ F] V [V ∧ F] = F v F = F

A = F e B = F

[A ∧ (¬B)] V [(¬A) ∧ (¬B)] = [F ∧ (¬F)] V [(¬F) ∧ (¬F)] = [F ∧ V] V [V ∧ V] = F v V = V

CERTO

B) A sequência de frases a seguir contém exatamente duas proposições.

< A sede do TRT/ES localiza-se no município de Cariacica.

< Por que existem juízes substitutos?

< Ele é um advogado talentoso.

Resolução:

Lembrando que para ser uma proposição, deve ser possível atribuir um valor lógico verdadeiro ou falso.

– A sede do TRT/ES localiza-se no município de Cariacica.

É uma proposição pois é possível atribuir verdadeiro ou falso.

– Por que existem juízes substitutos?

Claramente pergunta não é proposição.

– Ele é um advogado talentoso.

Não é proposição. É a chamada sentença aberta, onde para ser verdadeiro ou falso depende de quem é “ele”.

ERRADO

C) A proposição “Carlos é juiz e é muito competente” tem como negação a proposição “Carlos não é juiz nem é muito competente”.

Resolução

Considerando:

p: Carlos é juiz

q: Carlos é muito competente

Dessa forma, a proposição pode ser escrita como p ∧q. Assim, temos:

~(p ∧ q) = ~p v ~q

Assim, a negação de “Carlos é juiz e é muito competente” é “Carlos não é juiz ou não é muito competente”.

ERRADO

D) A proposição “A Constituição brasileira é moderna ou precisa ser refeita” será V quando a proposição

“A Constituição brasileira não é moderna nem precisa ser refeita” for F, e vice-versa.

Resolução:

Sejam:

P: A Constituição brasileira é moderna

Q: A Constituição brasileira precisa ser refeita

Assim:

“A Constituição brasileira é moderna ou precisa ser refeita” pode ser escrita assim: p v q . Negando temos:

~(p v q) = ~p ∧ ~q

Que pode ser escrita “A Constituição brasileira não é moderna nem precisa ser refeita”

CERTO

E) Para todos os possíveis valores lógicos atribuídos às proposições simples A e B, a proposição composta [A ∧ (¬B)] V B tem exatamente 3 valores lógicos V e um F.

Resolução:

Vamos testar para as quatro opções que temos:

A = V e B = V

[A ∧ (¬B)] V B = [V ∧ (¬V)] v V = [V ∧ F] v V = F v V = V

A = V e B = F

[A ∧ (¬B)] V B = [V ∧ (¬F)] v F = [V ∧ V] v F = V v F = V

A = F e B = V

[A ∧ (¬B)] V B = [F ∧ (¬V)] v V = [F ∧ F] v V = F v V = V

A = F e B = F

[A ∧ (¬B)] V B = [F ∧ (¬F)] v F = [F ∧ V] v F = F v F = F

CERTO

Questão 7 (TRT – CESPE).  Considere que cada uma das proposições seguintes tenha valor lógico V.

I Tânia estava no escritório ou Jorge foi ao centro da cidade.

II Manuel declarou o imposto de renda na data correta e Carla não pagou o condomínio.

III Jorge não foi ao centro da cidade.

A partir dessas proposições, avalie as afirmações A, B e C.

Considerações iniciais

Considerando:

T: Tânia estava no escritório

J: Jorge foi ao centro da cidade

M: Manuel declarou o imposto na data correta

C: Carla pagou condomínio

Resolução:

Podemos reescrever as proposições:

I) T V J = V

Como a proposição é verdadeira, o único caso que não pode ocorrer é T e J Falsas ao mesmo tempo.

II) M  ∧ ~C = V

Como a proposição é verdadeira, obrigatoriamente M é Verdadeira e C é Falsa.

III) ~ J = V

Como a proposição é verdadeira, J é Falsa.

A) “Manuel declarou o imposto de renda na data correta e Jorge foi ao centro da cidade” tem valor lógico V.

Para que M ∧ J = V devemos ter M = V e J = V

ERRADO

B) “Tânia não estava no escritório” tem, obrigatoriamente, valor lógico V.

Como J = F e T V J = V, a proposição T deve ser verdadeira, ou seja, Tania estava no escritório.

ERRADO

C) “Carla pagou o condomínio” tem valor lógico F.

Como M ∧ ~C = V, ~C deve ser Verdadeiro, ou seja, C é Falso.

CERTO

Questão 8 (RFB – ESAF). Considere a seguinte proposição: “Se chove ou neva, então o chão fica molhado”. Sendo assim, pode-se afirmar que:

a) Se o chão está molhado, então choveu ou nevou.

b) Se o chão está molhado, então choveu e nevou.

c) Se o chão está seco, então choveu ou nevou.

d) Se o chão está seco, então não choveu ou não nevou.

e) Se o chão está seco, então não choveu e não nevou.

Resolução

Temos 3 proposições:

P = Chove

Q = Neva

R = Chão molhado

Podemos escrever a proposição “Se chove ou neva, então o chão fica molhado” da seguinte forma:

P ou Q => R, que é equivalente a ~R => ~P e ~Q, ou seja, “Se o chão está seco, então não choveu e não nevou”

Resposta: D

Questão 9 (INSS – CESPE). Proposições são sentenças que podem ser julgadas como verdadeiras ou falsas, mas não admitem ambos os julgamentos. A esse respeito, considere que A represente a proposição simples “É dever do servidor apresentar-se ao trabalho com vestimentas adequadas ao exercício da função”, e que B represente a proposição simples “É  permitido ao servidor que presta atendimento ao público solicitar dos que o procuram ajuda financeira para realizar o cumprimento de sua missão”.

Considerando as proposições A e B acima, julgue os itens subseqüentes, com respeito ao Código de Ética Profissional do Servidor Público Civil do Poder Executivo Federal e às regras inerentes ao raciocínio lógico.

A) Represente-se por ¬A a proposição composta que é a negação da proposição A, isto é, ¬A é falso quando A é verdadeiro e ¬A é verdadeiro quando A é falso. Desse modo, as proposições “Se ¬A então ¬B” e “Se A então B” têm valores lógicos iguais.

Resolução

B ⇒ A é equivalente a ~A ⇒ ~B

Resposta: Errado

B) Sabe-se que uma proposição na forma “Ou A ou B” tem valor lógico falso quando A e B são ambos falsos; nos demais casos, a proposição é verdadeira. Portanto, a proposição composta “Ou A ou B”, em que A e B são as proposições referidas acima, é verdadeira.

Resolução

Basta notar que A = V e B = F

Resposta: Certo

C) A proposição composta “Se  A então  B” é necessariamente verdadeira.

Resolução

A proposição é falsa quando A = V e B = F

Resposta: Errado

Gostou dos nossos exercícios resolvidos sobre proposições lógicas?

Deixe o seu comentário.