Olá amantes da matemática! Atendendo a pedidos, hoje vou falar um pouco sobre as Transformações Lineares, conteúdo de nível superior, que faz parte do estudo da Álgebra Linear.
Para quem está vendo pela primeira vez pode parecer um pouco complexo, mas as transformações lineares são apenas funções naturais em um contexto de espaços vetoriais, tendo muitas aplicações na Física e nas Engenharias.
Bom estudo!
DEFINIÇÃO
A álgebra linear estuda funções cujos domínios e contradomínios são espaços vetoriais, e ainda preservam as operações de adição de vetores e de multiplicação de um vetor por um escalar.
Seja a função T:V → W, onde V e W são espaços vetoriais. Dizemos que a função T é uma transformação linear se possuir as seguintes propriedades:
I – T(x+y) = T(x) + T(y), onde x e y pertencem a V;
II – T(k.x) = k.T(x), onde x pertence a V e k pertence a R.
As propriedades I e II acima podem ser resumidas a uma propriedade apenas. Veja:
T(x + k.y) = T(x) + k.T(y), onde x e y pertencem a V e k pertence a R.
Por ser mais prática, utilizaremos esta caracterização das transformações lineares para mostrar se uma determinada função entre espaços vetoriais é uma transformação linear ou não, ou seja, sempre que a igualdade T(x + k.y) = T(x) + k.T(y) for verdadeira, a função será uma transformação linear.
Exemplo 1. Função T:R²→R, dada por T(x, y) = x + y.
Vamos verificar que a propriedade vale:
Sejam os vetores v=(a,b) e w=(c,d), pertencentes a R², e o escalar k pertencente a R. Temos:
T(v + k.w) = T((a,b) + k.(c,d))
T(v + k.w) = T((a,b) + (c.k,d.k))
T(v + k.w) = T((a,b) + k.(c,d))
T(v + k.w) = T(a+k.c, b+k.d)
T(v + k.w) = a + k.c + b + k.d
T(v + k.w) = a + b + k.c + k.d
T(v + k.w) = a + b + k(c + d)
T(v + k.w) = T(a,b) + k.T(c,d)
T(v + k.w) = T(x) + k.T(y)
Como podemos verificar, a propriedade vale para a função T, logo temos uma transformação linear de R² em R.
Exemplo 2. Função T:R→R, dada por T(x) = 10x.
Vamos verificar que a propriedade vale:
Sejam v e w pertencentes a R, e o escalar k. Temos:
T(v + k.w) = 10(v + k.w)
= 10v + 10.k.w
= T(v) + k.T(w).
Logo, T é uma transformação linear de R em R.
Exemplo 3. Função T:R²→R² dada por T(x, y) = (x², y).
Claramente não temos uma transformação linear devido ao x². Para provarmos basta acharmos um exemplo onde uma das propriedades não vale. Neste caso vamos verificar através da propriedade I.
Seja v = (1, 0) e w = (-1, 0)
T(v + w) = T((1,0) + (-1,0))
= T(1-1, 0+0)
= T(0, 0)
= (0², 0)
= (0, 0)
T(v) + T(w) = T(1,0) + T(-1,0)
= (1², 0) + ((-1)², 0)
= (1, 0) + (1, 0)
= (2, 0)
Nota-se que T(v + w) ≠ T(v) + T(w), logo a função T não é uma transformação linear.
Vejamos agora a propriedade abaixo, derivada as anteriores, que nos ajuda a identificar quando a função não é linear:
Se T : V → W é uma transformação linear então T(0) = 0.
Podemos concluir desta propriedade que se T(0) ≠ 0, então T não é uma transformação linear.
Da mesma forma, o fato de T(0) = 0 não é suficiente para afirmarmos que T é uma transformação linear (Exemplo 3).
Exemplo 4. Função T:R→R, dada por T(x) = x² + 1.
Calculando T(0):
T(0) = 0² + 1 = 1
Temos que T(0) ≠ 0, logo T não é linear.
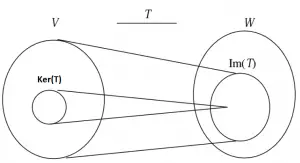
NÚCLEO E IMAGEM
NÚCLEO
Dada a transformação linear T:V→W, dizemos que o núcleo de T, denotado por Ker(T) ou N(T), é o conjunto de vetores de V que são transformados no vetor nulo por T, ou seja, Ker(T) = {v pertence a V, tal que T(v) = 0}.
Note que Ker(T) é um subconjunto não vazio de V, pois T(0)=0. E mais, Ker(T) também é um subespaço vetorial de V.
IMAGEM
Dada a transformação linear T:V→W, dizemos que a imagem de T, denotada por Im(T), é o conjunto de vetores W que estão associados a V através de T.
Como T(0)=0, Im(T) é um subconjunto não vazio de W. Mais ainda, é um subespaço vetorial de W.
Veja a figura:
TRANSFORMAÇÃO LINEAR INJETORA
Dizemos que a transformação linear T:V→W é injetora se, para quaisquer x,y pertencentes a V, se x≠y, então T(x)≠T(y). Isso equivale a dizer que se T(x)=T(y), então x=y.
Exemplo: T : R → R², dada por T(x) = (x+1,x).
Sejam k,z números Reais, onde k≠z. Temos:
T(k) = (k+1,k)
T(z) = (z+1,z)
Sabendo que k≠z, temos claramente que T(k)≠T(z).
TRANSFORMAÇÃO LINEAR SOBREJETORA
Dizemos que a transformação linear T:V→W é sobrejetora se, para todo w pertencente a W, existe v pertencente a V, onde T(v)=w. Isso equivale a dizer que Im(T)=W.
Exemplo: T : R² → R, dada por T(x,y) = x+y.
Para verificarmos que a transformação acima é sobrejetora, basta verificarmos que:
T(x,0) = x+0 = x
Nota-se um x real qualquer é sempre imagem de (x,0).
TRANSFORMAÇÃO LINEAR BIJETORA
Dizemos que uma transformação linear T:V→W é bijetora se for injetora e sobrejetora ao mesmo tempo. Nesses casos a transformação é chamada de isomorfismo e V e W são chamados de espaços vetoriais isomorfos.
OPERAÇÕES COM TRANSFORMAÇÕES LINEARES
ADIÇÃO
Sejam duas transformações lineares T:V→W e S:V→W. A soma de T e S, é a função T+S:V→W, onde
(T+S)(v) = T(v) + S(v)
MULTIPLICAÇÃO POR ESCALAR
Seja a transformação linear T:V→W e o escalar k Real. O produto entre o escalar e a função T é a função (kT):V→W, onde
(kT)(v) = k.T(v)
COMPOSIÇÃO
Sejam duas transformações lineares T:V→W e S:V→W. A Composta de T com S, nesta ordem, é a função ToS:V→W, onde
(ToS)(v) = T(S(v))
Então é isso pessoal. Espero que tenham aprendido um pouquinho com essas noções sobre as Transformações Lineares. Lembrando que para quem quer se aprofundar na matéria existem vários e vários teoremas, axiomas, definições e corolários que merecem ser vistos.
Até a próxima!
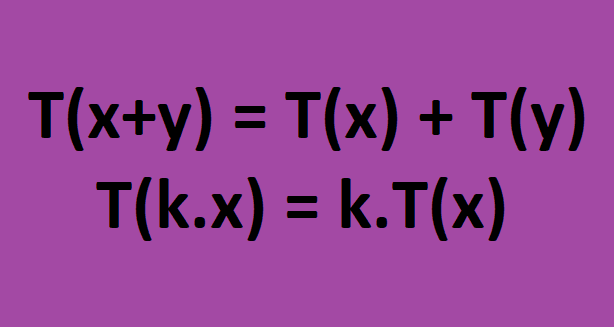
About Jordon.Bom dia.Parabéns pelo teu texto sobre Transformações Lineares,que ficou muito claro , objetivo e proveitoso.Continui postando temas matemáticos que muita gente vai aprender e gostar.Te sugiro postar o tema:Transformações Lineares e Matrizes.Obrigado.
Wilson
Olá, ótimo conteúdo, muito didático e bem apresentado. Obrigado pela postagem