Procurando exercícios resolvidos sobre conjuntos?

Este é o site certo.

Confira aqui uma seleção super especial de questões comentadas sobre a teoria de conjuntos, todas retiradas dos mais diversos concursos públicos realizados pelo país.

Bons estudos.

Questão 1 (Bombeiros MG – Igetec). Considere o conjunto A={x ∈ U | x satisfaz p}. Sobre A podemos afirmar:

a) Se x ∈ U então x ∈ A

b) Se x ∉ A então x ∉ U

c) Se x não satisfaz p então x ∉ A

d) U ⊂ A

Resolução:

Observe que a simbologia utilizada significa que para que um elemento x pertença ao conjunto A, ele deve pertencer ao conjunto universo U e satisfazer a propriedade p.

Basta interpretar a frase acima, se x não satisfaz a condição p ele nunca irá pertencer a A.

Resposta: C

Questão 2 (PM AC – Funcab). Sejam os conjuntos A = {1, 2, 3} e B = {2, 3, 5}, determine o conjunto A – B.

A) { }

B) {1, 5}

C) {5}

D) {1}

E) {2, 3}

Resolução

O conjunto A – B é formado pelos elementos que pertencem a A e não pertencem a B, ou seja, A – B = {1}

Resposta: D

Questão 3 (PM AC – Funcab). Considere o conjunto A = {1, 2, {3}} e assinale a alternativa que contém um sub conjunto de A.

A) {3}

B) {1, 3}

C) {2, 3}

D) {4, {3}}

E) {{3}}

Resolução

Um subconjunto de A é um conjunto que só contém elementos de A.

A dificuldade está em saber que o número 3 não é um elemento de A, e sim o conjunto {3}, assim descartamos as letras a, b e c.

Claramente o 4 não pertence a A, logo descartamos também a letra d.

Nos resta a letra E, que como vimos,  {3} pertence a A, logo  {{3}} é subconjunto de A.

Questão 4 (PF – Cespe). Em uma página da Polícia Federal, na Internet, é possível denunciar crimes contra os direitos humanos. Esses crimes incluem o tráfico de pessoas — aliciamento de homens, mulheres e crianças para exploração sexual — e a pornografia infantil — envolvimento de menores de 18 anos de idade em atividades sexuais explícitas, reais ou simuladas, ou exibição dos órgãos genitais do menor para fins sexuais.

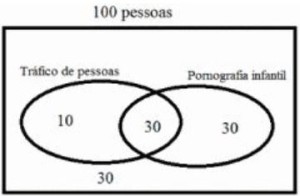
Com referência a essa situação hipotética e considerando que, após a análise de 100 denúncias, tenha-se constatado que 30 delas se enquadravam como tráfico de pessoas e como pornografia infantil; outras 30 não se enquadravam em nenhum desses dois crimes e que, em relação a 60 dessas denúncias, havia apenas a certeza de que se tratava de pornografia infantil, julgue os itens 57 e 58 subsequentes, acerca dessas 100 denúncias analisadas.

Analise as afirmações abaixo:

a) Dez denúncias foram classificadas apenas como crime de tráfico de pessoas.

Resposta: Certo (Veja a figura)

b) Os crimes de tráfico de pessoas foram mais denunciados que os de pornografia infantil.

Resposta: Errado (Veja a figura)

Questão 5 (PM SC – Cesiep). Leia as afirmações a seguir:

I. Os números Naturais são aqueles inteiros não positivos mais o zero.

II. Os números Irracionais são aqueles que representam dízimas periódicas.

III. Os números Reais representam a soma dos números Racionais com os Irracionais.

Assinale a alternativa correta:

a) Somente a assertiva II está correta.

b) Somente a assertiva III está correta.

c) Somente a assertiva I está correta.

d) Somente as assertivas II e III estão corretas.

Resolução:

I. Falsa – São os positivos…

II. Falsa – Podemos ter dízimas irracionais e irracionais que não são dízimas.

III. Correto – Os Reais é a união dos irracionais com os racionais.

Resposta: B

Questão 6 (PM Piauí – Nucepe). Considerando o conjunto universo U = {2, 4, 6, 8, 10} e os conjuntos não-vazios A e B, subconjuntos de U, tais que B ⊂A, A U B = {6, 8, 10} e A ∩ B = {8}, pode afirmar, CORRETAMENTE, que A é:

a) {6,8,10}

b) {4,6}

c) {4,6,8}

d) {2,6,10}

e) {6,8}

Resolução

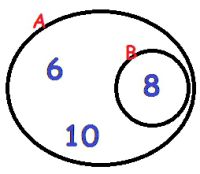
Basta observar o desenho, que atende as informações apresentadas.

A = {6, 8, 10}

Resposta: A

Questão 7 (PM Piauí – Nucepe). Dados os conjuntos:

A = {x∈R / 1 ≤ x < 10}

B = {x∈R / (x+1)(x-6) < 0}

C = {z∈R / z² = 6z}

O conjunto A ∩ (C ∪ B) é:

a) (-1, 7)

b) {3} ∪ (5, 7)

c) {0, 3}

d) (5, 7)

e) [1, 6]

Resolução

O conjunto A é formado pelos números Reais maiores ou iguais a 1 e menores que 10.

O conjunto B é formado pelos valores de x que fazem (x+1).(x-6) < 0. Resolvendo:

x² – 6x + x – 6 < 0

x² – 5x – 6 < 0

Vamos resolver a equação x² – 5x – 6 = 0

Utilizando o método da soma e produto:

Soma = -b/c = 5/1 = 5

Produto = c/a = -6/1 = -6

A solução é o conjunto composto pelo par de números cuja soma é 5 e o produto é -6.

Obviamente, os números que satisfazem são -1 e 6.

Se analisarmos o gráfico da função f(x) = x² – 5x – 6, temos uma parábola com cavidade para cima (a > 0) e com raízes -1 e 6, logo, o conjunto B é formado pelos números Reais maiores que -1 e menores que 6.

O conjunto C é formado pelos valores de z que fazem z² = 6z, ou seja, z = 0 ou z = 6.

Assim:

A = [1, 10[

B = ]-1, 6[

C = {0, 6}

Logo, A ∩ (C U B)  =  [1, 10[ ∩ ]-1, 6]  =  [1, 6]

Resposta: E

Questão 8 (PM ES – AOCP). Dados os conjuntos A = {1, 2, 3, 4} e B = {3, 4, 5}, então o número de elementos de A∪B é igual a:

(A) 3

(B) 4

(C) 5

(D) 6

(E) 7

Resolução

Os elementos do conjunto A∪B são aqueles que pertencem ao conjunto A ou pertencem ao conjunto B, sem a necessidade de repetição.

A∪B = (1, 2, 3, 4, 5)

Resposta: C

Questão 9 (UP). Sejam A = [0, 8], B = [2, +∞[ e o Universo U = R. Qual é o resultado da operação

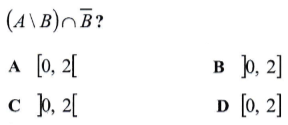
Resolução

Calculando A\B, os elementos que pertencem a A e não pertencem a B são representados pelo intervalo [0, 2[.

O complementar de B representa os números que não pertencem a B e estão no Universo R, ou seja, ]-∞, 2[.

Para finalizar, devemos calcular a interseção [0, 2[ ∩ ]-∞, 2[.

Veja que os números que pertencem aos dois intervalos podem ser representados pelo intervalo [0, 2[.

Resposta: A

Questão 10 (GCM SP – IBADE). A união de conjuntos é dada quando há a junção dos elementos dos mesmos. Considere um conjunto X com 55 elementos e um conjunto Y com 30 elementos. O menor número de elementos da união do conjunto X com o conjunto Y é: 

(A) 85. 

(B) 55. 

(C) 30. 

(D) 20. 

(E) 15.

Resolução

Observe que os conjuntos X e Y possuem 55 e 30 elementos, respectivamente.

A questão deseja saber o menor número possível de elementos da união X com Y. Isto acontece quando o conjunto Y, que possui menos elementos, estão contido no conjunto X. Neste caso, a união terá os 55 elementos de X.

Resposta: B

Gostou dos nossos exercícios resolvidos sobre conjuntos?

Deixe o seu comentário.