Procurando exercícios resolvidos sobre o famoso Teorema de Pitágoras?
Achou o site certo.
No sabermatemática você encontra uma seleção especial com várias questões comentadas, todas retiradas dos mais diversos concursos públicos realizados por todo o país.
Bons estudos!
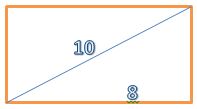
Questão 1 (PM ES 2013 – Exatus). A diagonal de um retângulo mede 10 cm, e um de seus lados mede 8 cm. A superfície desse retângulo mede:
a) 40 cm²
b) 48 cm²
c) 60 cm²
d) 70 cm²
e) 80 cm²
Resolução:
Desenhando o retângulo com as características informadas:
Para calcular a área precisamos saber a medida do outro lado, que pode ser descoberto pelo teorema de Pitágoras:
10² = 8² + x²
100 = 64 + x²
100 – 64 = x²
36 = x²
x = 6
Calculando a área do retângulo:
Área = 8.6 = 48 cm²
Questão 2. (Bombeiros ES 2011 – Cespe). Considerando que a área de um triângulo retângulo é igual a 30 cm² e a média aritmética das medidas de seus lados é igual a 10 cm, a afirmação abaixo está certa ou errada?
“O maior lado desse triângulo mede menos que 13,5 cm.”
Resolução:
Desenhando o triângulo com as características informadas:
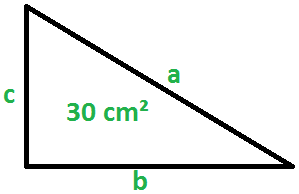
Como a média aritmética dos lados é igual a 10 cm:
(a + b + c) /3= 10
a + b + c = 30
Utilizando a fórmula da área do triângulo retângulo:
A = base x altura / 2
30 = b.c/2
b.c = 60
Pelo Teorema de Pitágoras:
a² = b² + c²
Temos
a + b + c = 30
30 – a = b + c
(30 – a)² = (b + c)²
30² – 2.30.a + a² = b² +2bc + c²
900 – 60a + a² = b² +2bc + c²
Sabendo do teorema de pitágoras podemos eliminar a² = b² + c². Vamos também substituir bc = 60:
900 – 60a = 2.60
60a = 900 – 120
60a = 780
a = 780/60
a = 13
CERTO
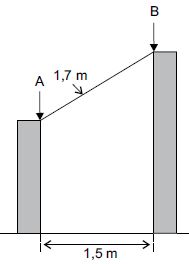
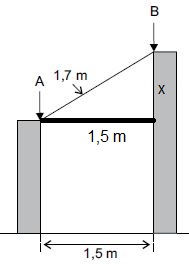
Questão 3. (PM SP 2014 – Vunesp). Duas estacas de madeira, perpendiculares ao solo e de alturas diferentes, estão distantes uma da outra, 1,5 m. Será colocada entre elas uma outra estaca de 1,7 m de comprimento, que ficará apoiada nos pontos A e B, conforme mostra a figura.
A diferença entre a altura da maior estaca e a altura da menor estaca, nessa ordem, em cm, é:
(A) 95.
(B) 75.
(C) 85.
(D) 80.
(E) 90.
Resolução:
Clique aqui para ver a resolução no YouTube.
Para resolvermos a questão, vamos localizar um triângulo retângulo na figura. Veja:
Note que x é exatamente a diferença que queremos, e podemos calculá-lo através do Teorema de Pitágoras:
1,7² = 1,5² + x²
2,89 = 2,25 + x²
x² = 2,89 – 2,25
x² = 0,64
x = 0,8 m ou 80 cm
Resposta: D
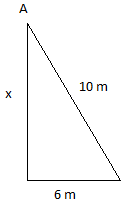
Questão 4 (SAP SP 2013). Roberto irá cercar uma parte de seu terreno para fazer um canil. Como ele tem um alambrado de 10 metros, decidiu aproveitar o canto murado de seu terreno (em ângulo reto) e fechar essa área triangular esticando todo o alambrado, sem sobra. Se ele utilizou 6 metros de um muro, do outro muro ele irá utilizar, em metros,
(A) 7.
(B) 5.
(C) 8.
(D) 6.
(E) 9.
Resolução:
A questão fala em cercar um canto murado, utilizando 10m de tela. Temos claramente um triângulo retângulo. Veja a figura:
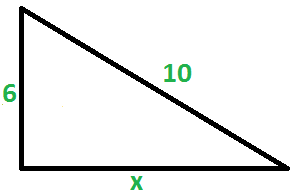
Basta utilizarmos o teorema de pitágoras, onde 10 é a hipotenusa, um cateto é 6 e o outro vamos chamar de x:
10² = 6² + x²
100 = 36 + x²
x² = 100 – 36
x² = 64
x = 8
Resposta: C
Questão 5 (PM Pará 2007 – Fadesp). Uma praça tem a forma de um triângulo ABC, retângulo em A, cuja hipotenusa a mede 250 metros e o cateto c mede 200 metros. Para garantir a execução de um serviço, houve necessidade de se interditar uma parte da praça com uma corda MN perpendicular à hipotenusa, distando 150 metros do vértice B, com M na hipotenusa e N no cateto c. O comprimento dessa corda, em metros, é
(A) 112,5.
(B) 125,5.
(C) 150,5.
(D) 175,5.
Resolução
Com as informações do enunciado, o formato da praça pode ser representado pela figura abaixo:
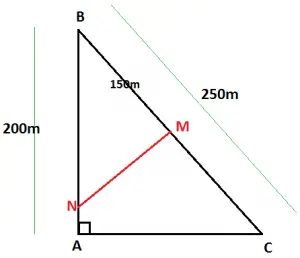
Nosso primeiro passo é acharmos o valor de AC através do teorema de Pitágoras:
BC² = AB² + AC²
250² = 200² + AC²
62500 = 40000 + AC²
AC² = 62500 – 40000
AC² = 22500
AC = 150
Pela semelhança dos triângulos ABC e MBN:
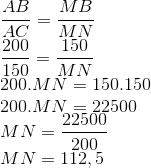
Resposta: A
Questão 6 (IBGE 2016 – Cesgranrio) Na Figura a seguir, PQ mede 6 cm, QR mede 12 cm, RS mede 9 cm, e ST mede 4 cm.
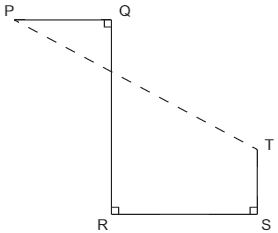
A distância entre os pontos P e T, em cm, mede
(A) 17
(B) 21
(C) 18
(D) 20
(E) 19
Resolução
Vamos marcar na figura as distâncias fornecidas e um ponto Z, de modo que tenhamos um triângulo retângulo onde PT é a medida da hipotenusa.
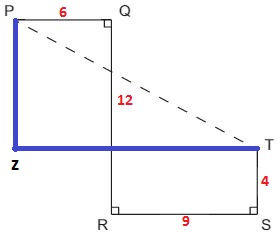
Como temos um triângulo retângulo iremos utilizar o famoso teorema de Pitágoras, onde:
PT = hipotenusa
PZ = 12 – 4 = 8
ZT = 6 + 9 = 15
PT² = 8² + 15²
PT² = 64 + 225
PT² = 289
PT = 17
Resposta: A
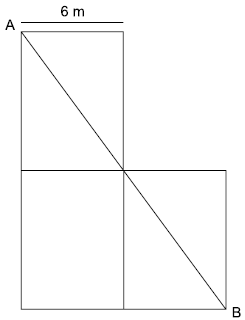
Questão 7 (TJ SP 2015 – Vunesp). Em um jardim, um canteiro de flores, formado por três retângulos congruentes, foi dividido em cinco regiões pelo segmento AB, conforme mostra a figura.
Se AB mede 20 m, então a área total desse canteiro é, em m2, igual a
(A) 162.
(B) 126.
(C) 135.
(D) 153.
(E) 144.
Resolução
Sabendo que os retângulos são congruentes e que AB = 20, vamos aplicar o teorema de pitágoras no triângulo abaixo:
Onde 6 e x são as medidas do retângulo.
10² = x² + 6²
100 = x² + 36
x² = 100 – 36
x² = 64
x = 8 m
Calculando a área do retângulo:
A = 6 x 8 = 48 m²
Como o canteiro é formado por 3 desses retângulos:
At = 3 x 48 = 144 m²
Resposta: E

E questão. Sobre matemática não sobre nãosobre namoro
Me ajudou muito obrigada por vocês eu passei de ano
Me ajudou muito obrigada por vocês eu passei de ano
Eu não entendi como resolver alguém pode me ajudar
Muito bom, me ajudou bastante. Pitágoras foi uma das minhas referências em meu tcc.
Obrigado pelo conteúdo!
Aqui tem ótimas dicas obrigado
Na questão 5, se a corda MN está a 150m do vértice B, não seria o triangulo formado por MNC?
Obs: sei que dessa forma nenhum as opções de resposta seria aceitável – mas, resta a dúvida. 🙂
Olá Hudson!
Sua observação é pertinente, porém as medidas fazem com que não tenhamos um triângulo MNC, mas um quadrilátero MNAC.