Você conhece a sequência de Fibonacci? Veja aqui a definição, propriedades e aplicações.
Bom estudo!
Definição
Uma das sequências numéricas mais importantes e intrigantes da matemática é a sequência de Fibonacci, que foi descoberta pelo matemático italiano Leonardo de Pisa, também conhecido como Fibonacci.
A sequência é a seguinte:
(1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …)
Observe que a partir do terceiro termo, cada elemento é exatamente igual a soma dois dois anteriores.
F3 = F2 + F1 = 1 + 1 = 2
F4 = F3 + F2 = 2 + 1 = 3
F5 = F4 + F3 = 3 + 2 = 5
F6 = F5 + F4 = 5 + 3 = 8
Generalizando, a sequência de Fibonacci é definida recursivamente pela fórmula:
F1 = F2 = 1
Fn = Fn-1 + Fn-2
Triângulo de Pascal
É possível extrair a sequência de Fibonacci do triângulo de Pascal. Os termos da sequência são formados pela soma das diagonais em vermelho na figura abaixo:

Número de Ouro
Veja o que acontece quando dividimos cada um dos termos da sequência de Fibonacci (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …) pelo seu antecessor:
1/1 = 1
2/1 = 2
3/2 = 1,5
5/3 = 1,6666…
8/5 = 1,6
13/8 = 1,625
21/13 ≅ 1,615384
34/21 ≅ 1,619048
…
Quanto mais divisões efetuarmos, mais próximos estaremos do número irracional 1.61803399…
Este número é conhecido como número de ouro, sendo representado pela letra grega phi.
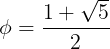
Representação Geométrica
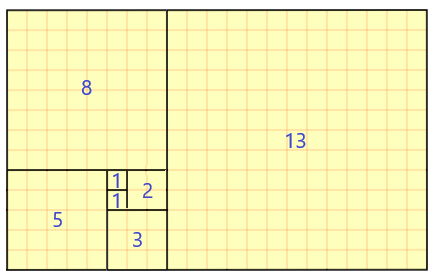
É possível observar a sequência de Fibonacci na figura abaixo, chamada de retângulo de ouro, que é formada por uma sequência de quadrados, cujas medidas dos lados representam exatamente a nossa sequência.
Desenhando arcos em cada um dos quadrados, formamos a chamada Espiral de Fibonacci:
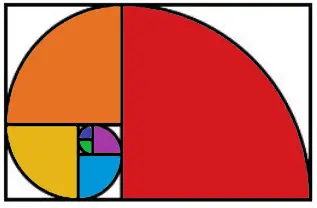
O mais interessante é que a Espiral de Fibonacci aparece diversas vezes na natureza:


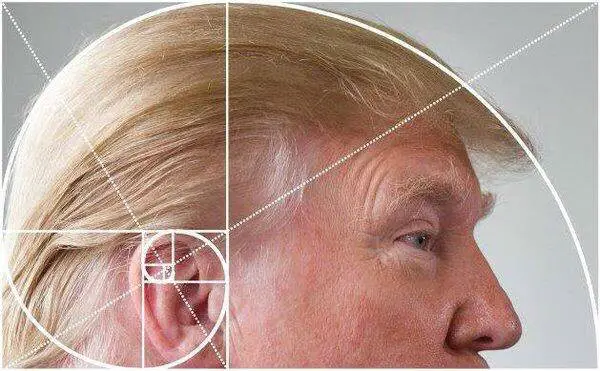
Podendo aparecer ainda em outros locais mais inusitados:
Gostou da sequência de Fibonacci?
Deixe o seu comentário.
