Dando continuidade ao estudo da geometria plana, hoje vamos estudar sobre a semelhança de triângulos, uma matéria importantíssima e que cai em praticamente todas as provas de concursos que cobram geometria plana.
É muito importante que o aluno esteja ciente das definições de triângulo, ângulo, medidas e proporcionalidade.
Bom estudo a todos.
Quando falamos em semelhança de triângulos, a primeira ideia que vem a cabeça é que vamos comparar triângulos. E é exatamente isso. Vamos aprender a identificar os casos de semelhança e como essa importante informação pode nos auxiliar na resolução de questões, e de problemas do dia a dia.
Existem duas condições para que dois triângulos sejam considerados semelhantes:
I – os ângulos correspondentes devem ser iguais (congruentes);
II – os lados correspondentes devem possuir medidas proporcionais.
Para que você possa entender melhor, dois triângulos são semelhantes quando são exatamente iguais ou quando um deles é uma versão reduzida do outro.
Veja um exemplo:
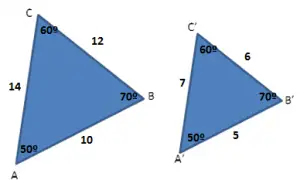
Na figura é possível observar que:
– Todos os ângulos correspondentes são congruentes:
A ≡ A’ ≡ 50°
B ≡ B’ ≡ 70°
C ≡ C’ ≡ 60°
– Todos os lados são proporcionais:
![]()
Comparar todos os lados e ângulos correspondentes é uma tarefa trabalhosa, por isso vamos apresentar uma forma mais simples. Basta verificar se eles se encaixam em um dos três casos de semelhança:
Caso AA
Dois triângulos são semelhantes quando possuem dois ângulos correspondentes congruentes.
Exemplo:
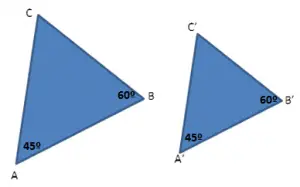
Neste caso temos dois triângulos onde dois pares de ângulos correspondentes são congruentes. Sabendo dessas informações, podemos concluir que todos são congruentes e que todos os lados correspondentes são proporcionais.
Caso LLL
Dois triângulos são semelhantes quando possuem os três lados correspondentes proporcionais.
Exemplo:
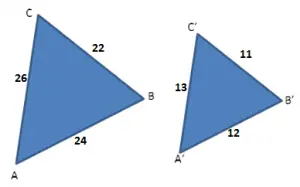
Neste caso temos dois triângulos onde todos os lados correspondentes são proporcionais. Sabendo disto, podemos concluir que os ângulos correspondentes são congruentes.
Caso LAL
Dois triângulos são semelhantes quando possuem dois lados correspondentes proporcionais, e os ângulos entre eles congruentes.
Exemplo:
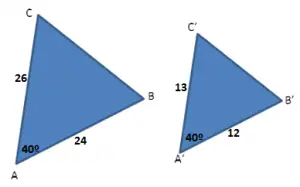
Neste caso, dois lados correspondentes proporcionais e os ângulos entre eles congruentes é suficiente para que os triângulos sejam semelhantes.
Então é isso pessoal… Espero que o conteúdo seja útil a todos os fiéis estudantes que acompanham o site.
Agora que você já aprendeu os conceitos, nada melhor do que praticar. Clique aqui para acessar a nossa página com exercícios resolvidos sobre este conteúdo.
