Procurando exercícios resolvidos sobre semelhança de triângulos?
Chegou no site certo.
Aqui a matemática é abordada de forma simples e objetiva.
Confira uma seleção especial de questões resolvidas, todas retiradas de concursos realizados por todo o país.
Bons estudos!
Questão 1 (CFO PM ES – Exatus). O soldado Ryan reside no 13 andar de um prédio de 15 andares. Sabe-se a distância entre o piso do andar onde mora o soldado Ryan e o piso térreo é de 39 m. Uma pessoa com altura de 1,8 m na parada ao lado desse edifício projeta uma sombra de 30 cm. Neste mesmo instante, a sombra projetada pelo edifício onde mora o soldado Ryan é igual a:
a) 7 m
b) 8 m
c) 9 m
d) 10 m
e) 11 m
Resolução:
Temos que Ryan mora no 13º andar e que a distância do seu piso até o piso térreo é de 39 metros.
Considerando que cada andar é da mesma altura, temos 12 andares mais o térreo, ou seja, 13 pavimentos.
Se são 39 metros, e 13 pavimentos, cada pavimento mede 3 metros de altura. Somando-se as alturas dos andares 13, 14 e 15, temos que o edifício mede 48 metros.
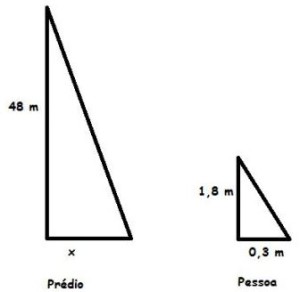
Sabendo que o sol forma o mesmo ângulo com o prédio e com a pessoa, podemos calcular usando semelhança de triângulos.
Veja a figura:
Resposta: B
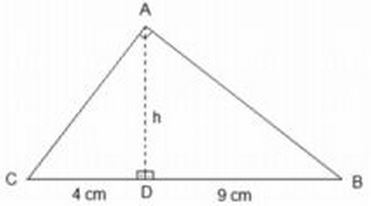
Questão 2 (PM ES – Funcab). A figura abaixo (meramente ilustrativa e fora de escala) representa um triângulo ABC retângulo em A, dividido em dois triângulos, ACD e ABD, ambos retângulos em D.
O valor, em cm, de AD = h, é:
A) 6 cm
B) 7,2 cm
C) 8 cm
D) 8,4 cm
E) 9 cm
Resolução:
Observe que os triângulos CDA e ADB são semelhantes.
Usando semelhança de triângulos:
Resposta: A
Questão 3 (PM Pará – Fadesp). Uma praça tem a forma de um triângulo ABC, retângulo em A, cuja hipotenusa a mede 250 metros e o cateto c mede 200 metros. Para garantir a execução de um serviço, houve necessidade de se interditar uma parte da praça com uma corda MN perpendicular à hipotenusa, distando 150 metros do vértice B, com M na hipotenusa e N no cateto c. O comprimento dessa corda, em metros, é
(A) 112,5.
(B) 125,5.
(C) 150,5.
(D) 175,5.
Resolução
Com as informações do enunciado, o formato da praça pode ser representado pela figura abaixo:
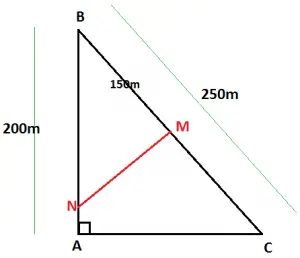
Nosso primeiro passo é acharmos o valor de AC através do teorema de Pitágoras:
BC² = AB² + AC²
250² = 200² + AC²
62500 = 40000 + AC²
AC² = 62500 – 40000
AC² = 22500
AC = 150
Pela semelhança dos triângulos ABC e MBN:
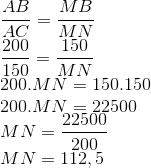
Resposta: A
Questão 4 (UP). Para construir a pipa representada na figura ao lado pelo quadrilátero ABCD, foram utilizadas duas varetas, linha e papel.
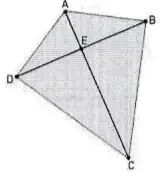
As varetas estão representadas pelos segmentos AC e BD. A linha utilizada liga as extremidades A, B, C e D das varetas, e o papel reveste a área total da pipa.
Os segmentos AC e BD são perpendiculares em E, e os ângulos ABC e ADC são retos. Se os segmentos AE e EC medem, respectivamente, 18 cm e 32 cm, determine o comprimento total da linha, representada por AB + BC + CD + DA.
a) 80 cm
b) 100 cm
c) 120 cm
d) 140 cm
Resolução
Considerando as informações do enunciado, temos a seguinte figura:
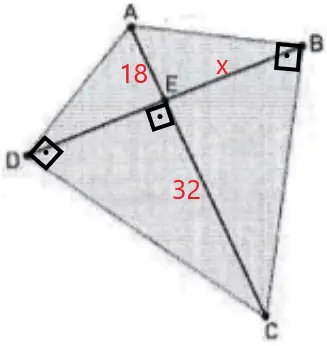
Observe os triângulos retângulos AEB e BEC. Podemos concluir que são triângulos semelhantes, pois:
- ambos possuem ângulos medindo 90°;
- os ângulos EBA e ECB são congruentes, pois ambos são complementares do ângulo EBC;
- por consequência, os ângulos EAB e EBC também são congruentes.
Considerando a semelhança de triângulos, e que x = EB, temos:
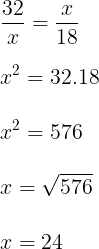
Podemos calcular os lados AB e BC através do Teorema de Pitágoras:
- No triângulo AEB:
AB² = 18² + 24²
AB² = 324 + 576
AB² = 900
AB = √900
AB = 30
- No triângulo BEC:
BC² = 24² + 32²
BC² = 576 + 1024
BC² = 1600
BC = √1600
BC = 40
Considerando as semelhanças de triângulo, temos que AB = DA e BC = CD.
Conclusão:
AB + BC + CD + DA = 30 + 40 + 40 + 30 = 140 cm
Resposta: D
Gostou dos nossos exercícios resolvidos sobre semelhança de triângulos?
Deixe o seu comentário.

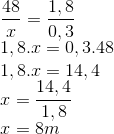
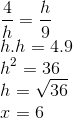
Calcule os valores de x e y:
48/12 = 72/18 = y/x
y=4 e x=1?
Existem infinitas soluções, onde y = 4x
Isso mesmo, existem infinitas possibilidades para x e y.
Basta seguir o esquema: (x * 4 = y)
Onde, y/x sempre será igual a 4, já que 48/12 é equivalente a 4 e o sinal sempre segue como “igual” (=)
mais 3+65*55= nao fasmal
O exercício 1 está incorreto. O anunciado diz que 39 metros é a distância entre o PISO do térreo e o PISO do 13º andar, ou seja, 39 são na verdade 12 andares. No total, 15 andares seriam 48,75m.
Rafael,
Entendemos que como ele cita piso do térreo, o primeiro andar começa a partir deste. Por isto 13 pavimentos.
Normalmente nos prédios o térreo é a garagem.
Boa noite,eu não entendi a número 1,por que da 48? Sendo que a soma de 13, 14 e 15 é igual a 42
Mariana,
Não estamos somando os números 13, 14 e 15.
Estamos somando 39 metros com a altura dos andares 13, 14 e 15, que medem 3 metros cada, resultando em 48 metros.
Poderia me ajudar nessa questão?
SE M e N são respectivamente os pontos médios dos lados AB e AC, os lados AB=4cm e AC= 6c de um triângulo ABC. Sabendo que as medianas CM e BN são perpendiculares, determine a medida da base BC.
aparentemente a sua 1 esta errada n
Olá João,
Poderia nos informar onde está o erro?
prestem atencao em relacao ao PISO galera
um quadrilatero ABCD TEM 63cm perimetro.as medidas dos lados AB,BC,CD e AD formam nessa ordem uma proporçao .
se AB=12cm e B=15cm quais sao as medidas das outras dois lados desse quadrilatero?
poderia me ajudar?
nessa 2 de de semelhança de triângulos porque é 4/h=h/9 …. não era pra ser 4/9??
Olá Kátia,
Não encontrei nenhum erro na resolução da questão.
Vdd tinha que ser 4/9 e h/h
TAMBÉM ACHO O MESMO PORQUE SÃO OS LADOS PROPORCIONAIS…
PORQUÊ ENTÃO 4/H=H/9?
Olá Edson!
Basta observar os ângulos congruentes.
A 1º questão está incorreta né? se tem 15 andares, e cada andar mede 3 metros, não deveria ser 45 metros. 15×3= 45.
Olá Leticia!
Através do enunciado é possível concluir que o térreo possui 3 metros de altura.