Confira aqui a prova resolvida de matemática e raciocínio lógico do concurso Sejus ES 2023, do concurso organizado pela banca Ibade para o cargo Inspetor Penitenciário.
Questão 21. Observe a matriz abaixo:
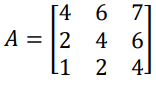
O determinante dessa matriz é:
(A) – 4
(B) – 2
(C) 0
(D) 2
(E) 4
Resolução:
Calcularemos o determinante da matriz quadrada A3x3 utilizando a Regra de Sarrus.
Locais onde você pode aprender mais sobre este assunto:
Como calcular o determinante de uma matriz 3×3 (escrito).
Como calcular o determinante de uma matriz 3×3 (YouTube).

DetA = 4.4.4 + 6.6.1 + 7.2.2 – 1.4.7 – 2.6.4 – 4.2.6
DetA = 64 + 36 + 28 – 28 – 48 – 48
DetA = 4
Resposta: E
Questão 22. Observe a imagem abaixo:
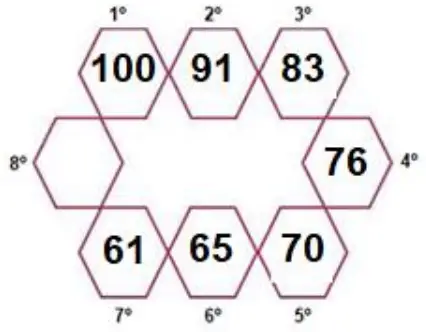
O 8º número dessa sequência é:
(A) 51
(B) 52
(C) 57
(D) 58
(E) 110
Resolução:
A primeira observação que devemos fazer em questões envolvendo sequências numéricas é verificar o padrão:
A diferença entre o primeiro e o segundo número é igual a 9.
A diferença entre o segundo e o terceiro número é igual a 8.
A diferença entre o terceiro e o quarto número é igual a 7.
…
A diferença entre o sexto e o sétimo número é igual a 4.
Observou o padrão?
A diferença entre o sétimo e o oitavo número deve ser igual a 3.
O oitavo número é: 61 – 3 = 58
Resposta: D
Questão 23. Considere a expressão abaixo:
log10(2x + 30) = 2, x > -15
O valor de x é:
(A) 35
(B) 45
(C) 70
(D) 80
(E) 100
Resolução
A questão será resolvida através da definição de logaritmos.
2x + 30 = 102
2x + 30 = 100
2x = 100 – 30
2x = 70
x = 70/2
x = 35
Resposta: A
Questão 24. Observe os triângulos semelhantes abaixo:
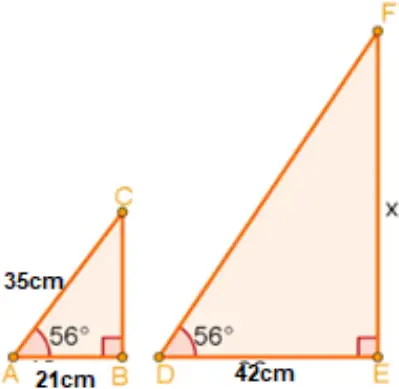
O valor de x é:
(A) 28
(B) 31
(C) 42
(D) 56
(E) 68
Resolução
Calcularemos inicialmente a medida de BC utilizando o Teorema de Pitágoras:
AC2 = AB2 + BC2
352 = 212 + BC2
1225 = 441 + BC2
BC2 = 1225 – 441
BC2 = 784
BC = √784
BC = 28
Considerando que são triângulos semelhantes, temos:
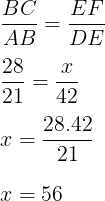
Resposta: D
Questão 25. Analise a proposição abaixo:
“Se Mateus estudou, então ele foi bem na prova.”
O conectivo lógico presente nessa proposição é de:
(A) negação;
(B) conjunção;
(C) disjunção;
(D) condicional;
(E) bicondicional.
Resolução
O conectivo lógico presente na proposição é o condicional, do tipo “Se p, então q”.
Clique aqui para aprender mais sobre os conectivos lógicos.
Resposta: D
Questão 26. Em um plano cartesiano há dois pontos:
A (5,2)
B (3,-1)
A distância entre os pontos A e B é:
(A) 5
(B) √5
(C) 2√5
(D) √9
(E) √13
Resolução
Marcando os pontos A e B no plano cartesiano, a distância entre eles pode ser calculada através do Teorema de Pitágoras, considerando que existe o triângulo ABJ abaixo:
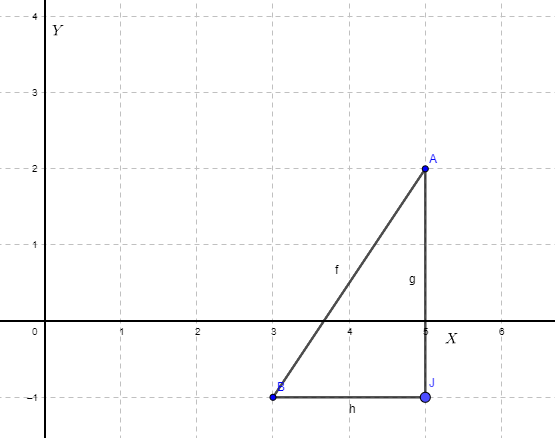
AB2 = BJ2 + AJ2
AB2 = 22 + 32
AB2 = 4 + 9
AB2 = 13
AB = √13
Resposta: E
Está gostando da resolução da prova da SEJUS ES 2023?
Clique aqui para assistir no YouTube.
Questão 27. Gabriel deseja fixar um cabo de sustentação em uma parede de modo que forme um ângulo de 30º com o chão, segundo o modelo abaixo:
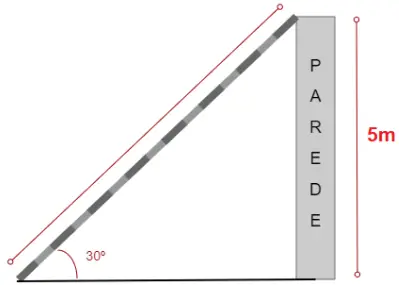
O tamanho do cabo de sustentação será de:
(A) 5
(B) 7
(C) 10
(D) 12
(E) 15
Resolução
Podemos calcular o tamanho do cabo, que chamaremos de x, com a informação de que sen30º = 1/2.
sen30º = cateto oposto / hipotenusa
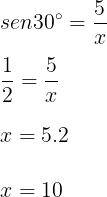
Resposta: C
Questão 28. Dona Maria possui uma confeitaria e deseja contabilizar seus gastos e lucros com a produção de doces. Para produzir certo tipo de doce, gasta-se R$ 4,50, em cada. A confeitaria vende esse doce por R$ 10,50. Além disso, há uma despesa fixa mensal de R$ 1500,00, que independe da quantidade de doce produzida. Dessa forma, a quantidade mínima de doces que deve ser vendida mensalmente para que a confeitaria passe a ter lucro é de:
(A) 200
(B) 225
(C) 250
(D) 275
(E) 300
Resolução
Observe que Dona Maria vende um doce por R$ 10,50 e gasta R$ 4,50, ou seja, ela possui um “lucro” de R$ 6,00 por doce. Porém, ela possui um custo fixo de R$ 1.500,00 por mês, ou seja, a função f que representa o lucro final da confeitaria pode ser expressa da seguinte forma:
f(x) = 6x – 1500
Agora que conhecemos a função lucro, podemos calcular a quantidade mínima para que a confeitaria tenha lucro:
f(x) > 0
6x – 1500 > 0
6x > 1500
x > 1500/6
x > 250
Observe que a Dona Maria passará a ter lucro vendendo 251 doces.
A questão pode ser anulada pois com 250 doces ela não tem lucro (e nem prejuízo).
Questão 29. Um casal deseja ter três filhos. A probabilidade de um deles não ter olhos azuis é de 1/4. Logo, a probabilidade de no máximo dois deles nascer com olhos azuis é de:
(A) 9/16
(B) 36/64
(C) 37/64
(D) 9/128
(E) 27/128
Resolução
A probabilidade de um filho não ter olhos azuis é de 1/4, ou seja, a probabilidade de ter olhos azuis é 3/4.
Deseja-se saber a probabilidade de, no máximo, dois deles nascerem com olhos azuis.
A expressão “no máximo dois” significa que a única opção que não serve para nós é a que todos nascem com olhos azuis. Vamos calcular a probabilidade de isto acontecer:
3/4 x 3/4 x 3/4 = 27/64
Como essa probabilidade não nos serve, faremos a subtração:
1 – 27/64
(64 – 27) / 64
37/64
Resposta: C
Questão 30. Fernanda foi a uma sorveteria e deseja comer quatro bolas de sorvete com sabores diferentes em qualquer ordem. Os sabores disponíveis são: chocolate, morango, uva, creme, flocos, limão, maracujá e caramelo. O número total de possibilidades que ela poderá combinar as bolas de sorvete será de:
(A) 24
(B) 35
(C) 70
(D) 94
(E) 140
Resolução
Fernanda pode escolher 4 entre 8 sabores.
Ela escolherá em qualquer ordem, ou seja, a ordem não é importante para ela.
Temos uma combinação de 8 elementos, tomados 4 a 4:
C8,4 = 8! / 4!.(8-4)!
C8,4 = 8! / 4!.4!
C8,4 = 8.7.6.5 / 4.3.2.1
C8,4 = 70
Resposta: C
Gostou da prova resolvida da Sejus ES 2023?
Deixe o seu comentário.
