Olá amigos estudantes. Nesta página vamos aprender a calcular o determinante de matrizes 3×3 através da Regra de Sarrus.

O cálculo é bem simples, basta seguir o passo a passo. Mesmo assim, é muito importante que o aluno tenha lido o nosso conteúdo sobre matrizes.

Bom estudo!

INTRODUÇÃO

Seja A uma matriz quadrada de ordem 3, ou seja, uma matriz com 3 linhas e 3 colunas.

Podemos representar o determinante de uma matriz 3×3 da seguinte forma:

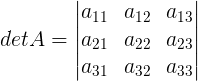
COMO CALCULAR

Vamos aprender em 3 passos a calcular o determinante de matrizes 3×3.

Primeiro passo: Repetir as duas primeiras colunas à direita da matriz:

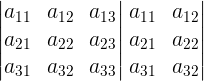
Segundo passo: Identificar as diagonais principais (cor vermelha) e as diagonais secundárias (cor azul):

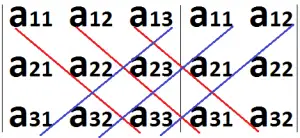
Terceiro passo: Multiplicar as diagonais e somar os resultados, sendo que as principais receberão o sinal positivo e as secundárias receberão o sinal negativo. Veja:

DetA = a₁₁.a₂₂.a₃₃ + a₁₂.a₂₃.a₃₁ + a₁₃.a₂₁.a₃₂ – a₃₁.a₂₂.a₁₃ – a₃₂.a₂₃.a₁₁ – a₃₃.a₂₁.a₁₂

EXEMPLO

Vamos praticar o que aprendemos para calcular o determinante da matriz 3×3 abaixo:

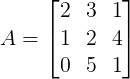
Repetindo as duas colunas à direita da matriz:

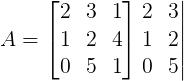
DetA = 2.2.1 + 3.4.0 + 1.1.5 – 0.2.1 – 5.4.2 – 1.1.3

DetA = 4 + 0 + 5 – 0 – 40 – 3

DetA = -34