Confira aqui a prova resolvida do concurso para a Polícia Militar do Estado de São Paulo (PM – SP), para o cargo de Oficial. Edital publicado em 2020 e prova aplicada em 2021 pela FGV.
Gabarito Extraoficial!!!!!!
Questão 45. Em certa cidade, o número de furtos de automóveis em maio de 2020 foi 40% menor do que em janeiro de 2020. De maio de 2020 para janeiro de 2021, houve um aumento de 45% no número de furtos de automóveis.
Nessa cidade, de janeiro de 2020 para janeiro de 2021, com relação ao número de furtos de automóveis, houve
(A) um aumento de 5%.
(B) um aumento de 12,5%.
(C) um aumento de 15%.
(D) uma redução de 13%.
(E) uma redução de 15%.
Resolução
- O número de furtos de automóveis em maio de 2020 foi 40% menor do que em janeiro de 2020, ou seja, o número de furtos de maio/2020 foi igual a 60% do número de furtos de janeiro/2020.
Neste caso, o número de furtos “foi multiplicado” por 0,60.
- De maio de 2020 para janeiro de 2021, houve um aumento de 45% no número de furtos, ou seja, o número de furtos em janeiro/2021 foi igual a 145% do número de furtos em maio /2020.
Neste caso, o número de furtos “foi multiplicado” por 1,45.
Como queremos saber o que aconteceu de janeiro de 2021 para janeiro de 2021, basta multiplicarmos 0,60 por 1,45:
0,60 . 1,45 = 0,87 = 87%
Como o número de furtos em janeiro/2021 representa 87% do número de furtos em janeiro/2020, podemos concluir que houve uma redução de 13%.
Resposta: D
Questão 46. 180 soldados serão posicionados no pátio do quartel, arrumados em linhas e colunas, de maneira a formar um retângulo perfeito. Sabe-se que tanto o número de linhas quanto o número de colunas do retângulo não podem ser menores que 5.
O maior número de arrumações possíveis para esse retângulo de soldados é
(A) 4.
(B) 5.
(C) 7.
(D) 10.
(E) 12.
Resolução
Fatorando o 180, temos:
180 = 2².3².5
Devemos organizar os soldados, de modo que os lados do retângulo sejam maiores ou iguais a 5. Para tal análise, consideraremos a fatoração de 180.
- Considerando um lado igual a 5, o outro lado será 2².3² = 36.
- Considerando um lado igual a 10 (2.5), o outro lado será 2.3² = 18
- Considerando um lado igual a 20 (2².5), o outro lado será 3² = 9
- Considerando um lado igual a 15 (3.5), o outro lado será 2².3 = 12
- Considerando um lado igual a 30 (2.3.5), o outro lado será 2.3 = 6
- Considerando um lado igual a 45 (3².5), o outro lado será 2² = 4
Veja que temos 6 retângulos diferentes. Devemos apenas observar que, quando os soldados estão organizados, um retângulo de 5 x 36, por exemplo, é diferente de um retângulo de 36 x 5, ou seja, ao invés de 6 arrumações, temos 12 arrumações possíveis.
Resposta: E
Questão 47. Em um grupo de N pessoas, há 12 homens a mais do que mulheres. Retirando-se 6 homens desse grupo, a razão entre o número de homens e o número de mulheres passa a ser de 7/5.
O valor de N é
(A) 36.
(B) 42.
(C) 45.
(D) 48.
(E) 54.
Resolução
Considere:
h = quantidade de homens
m = quantidade de mulheres
- Como há 12 homens a mais do que mulheres, temos que:
h = m + 12
- Como retirando-se 6 homens desse grupo, a razão entre o número de homens e o número de mulheres passa a ser de 7/5, temos que:
(h – 6) / m = 7/5
(h – 6).5 = 7m
5h – 30 = 7m
Temos duas equações. Substituindo o valor de h na segunda equação:
5h – 30 = 7m
5(m + 12) – 30 = 7m
5m + 60 – 30 = 7m
5m + 30 = 7m
30 = 7m – 5m
2m = 30
m = 30/2
m = 15
Calculando o valor de h:
h = m + 12
h = 15 + 12
h = 27
Finalizando:
N = h + m
N = 27 + 15
N = 42
Resposta: B
Questão 49. Joana pagou uma conta vencida, com juros de 5%, no valor total (juros incluídos) de R$ 382,20. Se Joana tivesse pagado a conta até o vencimento, teria economizado
(A) R$ 18,20.
(B) R$ 19,11.
(C) R$ 20,32.
(D) R$ 20,60.
(E) R$ 21,22.
Resolução
Seja x o valor inicial da conta paga por Joana. Como foram cobrados 5% de juros, temos que:
x . 1,05 = 382,20
x = 382,20 / 1,05
x = 364,00
Calculando os juros pagos por Joana:
382,20 – 364,00 = R$ 18,20
Resposta: A
Questão 50. Considere todos os anagramas da palavra BRASIL.
O número de anagramas que não têm as vogais juntas é
(A) 720.
(B) 600.
(C) 480.
(D) 240.
(E) 120.
Resolução
Considerando que não existem letras repetidas, a quantidade total de anagramas da palavra BRASIL é:
6! = 6.5.4.3.2.1 = 720
Calcularemos a quantidade de anagramas da palavra BRASIL que possuem vogais juntas, considerando que existem apenas duas (A e I).
Considerando AI como apenas uma letra, a quantidade de anagramas será:
5! = 5.4.3.2.1 = 120
Como podemos inverter as duas vogais, ou seja, AI é diferente de IA, temos 240 anagramas da palavra BRASIL com as vogais juntas.
A quantidade de anagramas que não possuem vogais juntas será exatamente a diferença:
720 – 240 = 480
Resposta: C
Questão 51. Ao resolver certo problema, encontramos a equação exponencial ax = 100.
Sabendo que o logaritmo decimal de “a” é igual a 0,54, o valor de “x” é, aproximadamente,
(A) 2,8.
(B) 3,1.
(C) 3,4.
(D) 3,7.
(E) 4,2.
Resolução
Aplicando o logaritmo decimal em ambos os lados da equação:
log(ax) = log100
x.loga = 2
x.0,54 = 2
x = 2/0,54
x = 3,7
Resposta: D
Questão 52. Para abastecer os carros da corporação, há um tanque cilíndrico de combustível, com 2 m de diâmetro e 1,5 m de altura.
A capacidade desse tanque é de, aproximadamente,
(A) 4.100 litros.
(B) 4.400 litros.
(C) 4.700 litros.
(D) 5.000 litros.
(E) 5.300 litros.
Resolução
O volume de um cilindro pode ser calculado pelo produto da área da base pela altura (clique aqui para saber mais).
Calculando a área da base, considerando o raio igual a 1m (metade do diâmetro), temos:
A = π.r²
A = 3,14.1²
A = 3,14
Calculando o volume:
V = 3,14 . 1,5
V = 4,71 m³
Para finalizar, devemos apenas saber que 1m³ equivale a 1 mil litros, ou seja, o tanque tem capacidade para aproximadamente 4710 litros de combustível.
Observação: a diferença ocorre devido a aproximação utilizada no número π.
Resposta: C
Questão 53. Em certa cidade, verificou-se que a quantidade de assaltos ocorridos em cada mês era inversamente proporcional ao número de policiais presentes no patrulhamento das ruas nesse mês.
Sabe-se que, em abril, 400 policiais estiveram presentes no patrulhamento e 30 assaltos ocorreram, e que, em maio, o
número de assaltos caiu para 24.
O número de policiais que estiveram presentes no patrulhamento no mês de maio foi
(A) 320.
(B) 360.
(C) 420.
(D) 460.
(E) 500.
Resolução
A questão pode ser resolvida através da regra de três simples, considerando que temos duas grandezas inversamente proporcionais:

24 . x = 400 . 30
24x = 12000
x = 12000 / 24
x = 500
Resposta: E
Questão 54. Considere a equação x² + x – 3 = 0.
A soma dos cubos das raízes dessa equação é
(A) −1.
(B) −10.
(C) −27.
(D) um número real irracional.
(E) um número complexo imaginário.
Resolução
Temos uma equação do segundo grau.
Calculando o valor de delta:
Δ = b² – 4ac
Δ = 1² – 4.1.(-3)
Δ = 1 + 12
Δ = 13
Calculando as raízes:
x = (-b +- √Δ)/2a
x = (-1 +- √13)/2.1
x = (-1 +- √13)/2
- x’ = (√13 – 1)/2
- x” = (-1 – √13)/2 = -(√13 + 1)/2
A questão deseja saber o valor da soma dos cubos das raízes.
Podemos calcular o cubo através dos produtos notáveis cubo da soma e cubo da diferença, onde:
(a + b)³ = a³ + 3a²b + 3ab² + b³
(a – b)³ = a³ – 3a²b + 3ab² – b³
Ignorando inicialmente o denominador das raízes, observe que uma possui o formato -(a + b)³ e outra possui o formato (a – b)³ (considerando a = √13 e b = 1):
-(a + b)³ = – a³ – 3a²b – 3ab² – b³
(a – b)³ = a³ – 3a²b + 3ab² – b³
Somando os dois cubos:
Soma = – a³ – 3a²b – 3ab² – b³ + a³ – 3a²b + 3ab² – b³
Soma = – 6a²b – 2b³
Substituindo os valores de a e b:
Soma = – 6a²b – 2b³
Soma = – 6(√13)².1 – 2.1³
Soma = – 6.13.1 – 2
Soma = – 78 – 2
Soma = – 80
Veja que a soma dos cubos das raízes da equação é exatamente igual a -80, quando consideramos apenas os numeradores.
Observe que o numerador de ambas as raízes é 2, que elevado ao cubo é igual a 8, ou seja, a soma dos cubos das raízes da equação dada é igual a:
-80 / 8 = -10
Resposta: B
Questão 55. A figura a seguir mostra a quadra retangular ABCD de um quartel, com 30 m de comprimento e 21 m de largura, dividida em quadrados iguais.
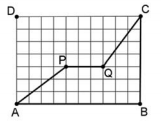
Dois soldados, Pedro e Paulo, caminharam de A até C por caminhos diferentes: Pedro percorreu os lados AB e BC, e Paulo percorreu os segmentos AP, PQ e QC.
É correto concluir que
(A) Pedro percorreu 12 m a mais que Paulo.
(B) Pedro percorreu 12 m a menos que Paulo.
(C) Pedro percorreu 4 m a mais que Paulo.
(D) Pedro percorreu 4 m a menos que Paulo.
(E) Pedro e Paulo percorreram distâncias iguais.
Resolução
Observando a figura e as medidas informadas no enunciado da questão, podemos concluir que cada um dos quadradinhos possui lado equivalente a 3 metros.
Calculando a medida do percurso de Pedro:
AB = 30 metros
BC = 21 metros
Total: 30 + 21 = 51
Calculando a medida do percurso de Paulo:
- AP é a hipotenusa de um triângulo retângulo de catetos medindo 9 e 12, ou seja, temos uma terna pitagórica e podemos concluir que AP = 15 metros.
Obs: Quem não tem conhecimento das ternas pitagóricas pode utilizar o Teorema de Pitágoras.
- PQ = 9 metros
- QC também é a hipotenusa de um triângulo de catetos iguais a 9 e 12, ou seja, QC = 15 metros.
Total: 15 + 9 + 15 = 39 metros
Diferença:
51 – 39 = 12 metros
Pedro andou 12 metros a mais que Paulo.
Resposta: A
Questão 56. O retângulo ABCD da figura a seguir tem as dimensões AB = 10 e BC = 6.
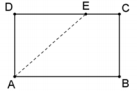
O ponto E do lado CD é tal que o segmento AE divide o retângulo em duas partes de forma que a área de uma seja o dobro da área da outra.
O segmento DE mede
a) 13/2
b) 16/3
c) 20/3
d) 21/4
e) 25/4
Resolução
Sabendo que AB = 10, considere DE = x e EC = 10 – x.
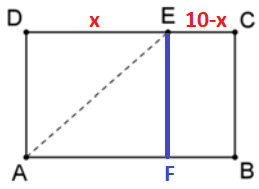
Como o nosso objetivo é dividir a figura em duas partes, que modo que ABEC tenha o dobro da área de ADE, e sabendo ainda que ADE e AEF possuem a mesma área, podemos concluir que as áreas do triângulo ADE e do retângulo ECFB devem ser iguais.
AADE = 6x/2 = 3x
AECFB = 6(10 – x) = 60 – 6x
Igualando as duas áreas:
3x = 60 – 6x
3x + 6x = 60
9x = 60
x = 60/9
x = 20/3
Resposta: C
Gostou da prova resolvida (gabarito extraoficial) da PM SP 2021, para o cargo de Oficial?
Deixe o seu comentário.
