Estudando matemática para concursos? Confira aqui a prova resolvida do concurso Banco do Brasil (BB) 2018, realizado pela Fundação Cesgranrio.

O concurso é regulado pelo EDITAL Nº 01 – 2018/001, e possui vagas para os estados de SP, RJ e DF.

Boa sorte!

11. Para x > 0, seja S_x a soma

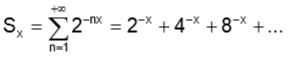
O número real x para o qual se tem S_x = 1/4 é

(A) 4

(B) log₂5

(C) 3/2

(D) 5/2

(E) log₂3

Resolução

Veja que S_x é o somatório de uma P.G. Infinita.

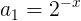
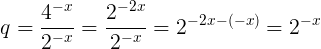
Utilizando a fórmula da soma de uma P.G. Infinita, onde sabemos que o resultado é 1/4, temos:

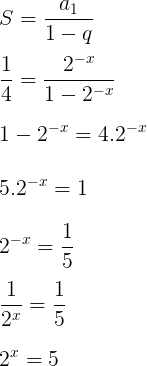
Pela definição de logaritmos:

x = log₂5

Resposta: B

12. O dono de uma loja deu um desconto de 20% sobre o preço de venda (preço original) de um de seus produtos e, ainda assim, obteve um lucro de 4% sobre o preço de custo desse produto.

Se vendesse pelo preço original, qual seria o lucro obtido sobre o preço de custo?

(A) 40%

(B) 30%

(C) 10%

(D) 20%

(E) 25%

Resolução

x =  preço original

y = preço de custo

Pela informação do enunciado temos:

x.0,8 = 1,04.y

x = 1,04.y/0,8

x = 1,3y

Veja que o preço original é 30% maior que o preço de custo.

Resposta: B

13. Sabe-se que g é uma função par e está definida em todo domínio da função f, e a função f pode ser expressa por f(x) = x² + k.x . g(x).

Se f(1) = 7, qual o valor de f(-1)?

(A) 7

(B) 5

(C) – 7

(D) – 6

(E) – 5

Resolução

Sabendo que  f(1) = 7, temos:

f(x) = x² + k.x . g(x)

7 = 1² + k.1 . g(1)

7 = 1 + k.g(1)

7 – 1 = k.g(1)

k.g(1) = 6

Como g é par, g(1) = g(-1), de onde podemos concluir que:

k.g(-1) = 6

Calculando o valor de f(-1):

f(x) = x² + k.x . g(x)

f(-1) = (-1)² + k.(-1).g(-1)

f(-1) = 1 – k.g(-1)

Sabendo que k.g(-1) = 6:

f(-1) = 1 – 6

f(-1) = – 5

Resposta: E

14. Considere o conjunto A cujos 5 elementos são números inteiros, e o conjunto B formado por todos os possíveis produtos de três elementos de A.

Se B = {-30, -20, -12, 0, 30}, qual o valor da soma de todos os elementos de A?

(A) 5

(B) 3

(C) 12

(D) 8

(E) -12

Resolução

Veja que os elementos de B são produtos de 3 elementos de A.

Como 0∈B, podemos concluir que 0∈A, pois zero multiplicado por quaisquer dois elementos de A é igual a zero.

Os outros 4 elementos, ao serem multiplicados 3 a 3, devem reproduzir os outros 4 elementos de B.

Fatorando os elementos de B:

30 = 2.3.5

20 = 2.2.5

12 = 2.2.3

Analisando os demais elementos do conjunto B e a fatoração de cada um deles, podemos concluir que os 4 elementos restantes do conjunto A são:

-2, 2, 3, 5

Veja:

-30 = -2.3.5

-20 = -2.2.5

-12 = -2.2.3

30 = 2.3.5

A = {-2, 0, 2, 3, 5}

Soma:

-2 + 0 + 2 + 3 + 5 = 8

Resposta: D

15. Uma sequência numérica tem seu termo geral representado por a_n, para n ≥ 1. Sabe-se que a₁ = 0 e que a sequência cujo termo geral é b_n = a_n+1 – a_n, n ≥ 1, é uma progressão aritmética cujo primeiro termo é b₁ = 9 e cuja razão é igual a 4.

O termo a₁₀₀₀ é igual a

(A) 2.002.991

(B) 2.002.995

(C) 4.000.009

(D) 4.009.000

(E) 2.003.000

Resolução

Listando os termos de b_n:

b₁ = a₂ – a₁

b₂ = a₃ – a₂

b₃ = a₄ – a₃

…

b₉₉₉ = a₁₀₀₀ – a₉₉₉

Somando as equações acima, vários termos de a_n se anulam, tendo como resultado:

b₁ + b₂ + b₃ + … + b₉₉₉ = a₁₀₀₀ – a₁

b₁ + b₂ + b₃ + … + b₉₉₉ = a₁₀₀₀ – 0

b₁ + b₂ + b₃ + … + b₉₉₉ = a₁₀₀₀

Veja que o resultado que queremos é a soma dos 999 primeiros termos de b_n.

Calculando b₉₉₉ através da fórmula do termo geral:

b_n = b₁ + (n – 1).r

b₉₉₉ = 9 + (999 – 1).4

b₉₉₉ = 9 + 998.4

b₉₉₉ = 9 + 3992

b₉₉₉ = 4001

Calculando a soma dos 999 primeiros termos da P.A. b_n:

S = (b₁ + b_n).n/2

S = (b₁ + b₉₉₉).999/2

S = (9 + 4001).999/2

S = 4010.999/2

S = 2002995

Resposta: B

Gostou da prova do Banco do Brasil (BB) 2018 resolvida?

Deixe o seu comentário.