Progressão Geométrica

Você sabe o que é uma Progressão Geométrica (PG)? Nesta página veremos tudo o que você precisa saber sobre este tipo de progressão, apresentando a definição, fórmulas e vários exemplos.

O conteúdo é muito importante e está presente em praticamente todas as provas de concursos públicos, vestibulares ou Enem.

Bons estudos!

Introdução

Observe a sequência de números abaixo:

1, 2, 4, 8, 16, 32, 64, …

É possível observar que existe um padrão. Cada número, com exceção do primeiro, é sempre o dobro do anterior.

Da mesma forma, poderíamos ter apresentado uma sequência onde cada número é o triplo, quádruplo ou quíntuplo do anterior.

Qualquer sequência com esse atributo é chamada de Progressão Geométrica (PG).

Definição

Podemos definir Progressão Geométrica (PG), como uma sucessão de números reais não nulos, obtida multiplicando o número anterior por um valor fixo, onde esse valor é chamado de razão representado pela letra q.

Vejamos alguns exemplos de PG:

Exemplo 1:

1, 2, 4, 8, 16, … (q = 2)

Exemplo 2:

2, 20, 200, 2000, … (q = 10)

Exemplo 3: 

2, 2, 2, 2, … (q = 1)

Exemplo 4:

1, -1, 1, -1, … (q = -1)

Termo Geral da PG

Assim como em uma PA, conhecendo o primeiro termo (a₁) e a razão (q) da PG, é possível descobrir qualquer elemento da sequência.

Veja a fórmula:

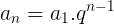
Essa expressão simples é capaz de determinar qualquer termo (a_n), sabendo-se o primeiro termo e a razão.

Vamos utilizá-la em alguns exemplos:

Exemplo 5:

Calcular o 10º termo da sequência (5, 10, 20, 40,…)

Temos que a₁ = 5, n = 10 e q = 2.

Utilizando a fórmula do termo geral:

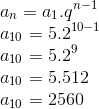
Exemplo 6:

Calcular o 6º termo da sequência (3, 9, 27,…)

Temos que a₁ = 3, n = 6 e q = 3.

Utilizando a fórmula do termo geral:

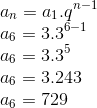
Soma dos termos de uma PG finita

A soma dos termos de uma PG finita pode ser facilmente calculada conhecendo o primeiro termo, a quantidade de termos e a razão.

Veja a fórmula:

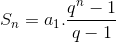
Obs: A fórmula não é valida para q = 1 para evitarmos divisão por zero.

Vejamos alguns exemplos de como utilizar a fórmula para somar progressões geométricas finitas:

Exemplo 7:

Calcular a soma dos 10 primeiros termos da PG (1,2,4,8,…):

Nota-se que o primeiro termo é 1, a razão é 2 e a quantidade de termos é 10.

Utilizando a fórmula:

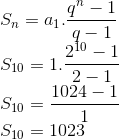
Exemplo 8:

Calcular o valor da soma 2+6+18+54+162+486+1458+4374

Trata-se da soma dos 8 primeiros termos de uma P.G. onde a₁=1, q=3 e n=8.

Utilizando a fórmula:

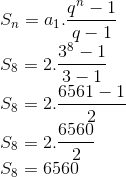
Soma dos termos de uma PG infinita

Vejamos o exemplo abaixo de uma Progressão Geométrica com infinitos termos:

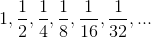
Nota-se que o termo da PG está ficando cada vez menor, isto acontece porque a razão da PG é 1/2.

Sempre que a razão é um número real entre -1 e 1, a tendência é que a PG se aproxime cada vez mais de zero.

A soma dos termos de uma PG infinita pode ser calculada através da fórmula abaixo, desde que -1<q<1.

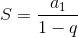
Vamos utilizar a fórmula para somar todos os termos da PG infinita citada acima:

Temos que a₁ = 1 e q = 1/2

Utilizando a fórmula:

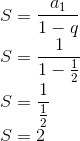
Gostou do nosso conteúdo sobre as Progressões Geométricas? Deixe o seu comentário.

Até a próxima!