Estudando matemática para concursos? Confira aqui vários exercícios resolvidos sobre progressões geométricas, também conhecidas como PGs.
Todas as questões foram retiradas de provas de concursos e traduzem fielmente o que a banca espera que o candidato saiba sobre o assunto.
Bom estudo!
Questão 1 (PM SC – Cesiep). Com base na seguinte progressão geométrica: {2; 4; 8; 16; 32; 64;… } o próximo valor da sequência seria:
a) 96
b) 128
c) 92
d) 144
Resolução
Basta observar que a razão da PG é 2, ou seja, para acharmos o próximo basta multiplicar por 2.
Então, 64 x 2 = 128
Resposta: B
Questão 2 (Bombeiros ES – Cespe). Um soldado, um sargento e um tenente têm suas idades, em anos, dispostas em progressão geométrica, sendo o soldado o mais novo dos três, e o tenente, o mais velho. Sabendo que o produto dessas idades, em anos, é 27.000 e que a soma das idades do sargento e do tenente é 75 anos, julgue a afirmação abaixo:
“A idade do sargento é superior a 32 anos”
Resolução:
Sabendo que as idades do soldado, do sargento e do tenente estão em progressão geométrica, nesta ordem, as idades dos mesmos serão:
Soldado = x/y
Sargento = x
Tenente = xy
onde y é a razão da P.G.
Como o produto das idades é 27000:
x/y . x . xy = 27000
x³ = 27000
x = 30
Sabendo que a idade do sargento é 30, e que a soma das idades do sargento mais tenente é 75, temos que a idade do tenente é 45, ou seja,
xy = 45
30y = 45
y = 45/30
y = 1,5
A idade do soldado é:
30/1,5 = 20
Assim:
Soldado: 20 anos
Sargento: 30 anos
Tenente: 45 anos
A idade do sargento é superior a 32 anos.
Resposta: ERRADO
Questão 3 (PM PE – IAUPE). Uma fábrica inaugurou sua produção com 4 itens. Sabendo-se que a quantidade de itens produzidos pela fábrica em cada ano consecutivo obedece a uma progressão geométrica e que, no quinto ano, foram produzidos 324 itens, qual a soma total de itens fabricados nesses cinco primeiros anos?
A) 434
B) 844
C) 448
D) 848
E) 484
Resolução
Temos uma fábrica que a quantidade de itens produzidos anualmente cresce em progressão geométrica, sendo que no primeiro ano, a fábrica produziu 4 itens, e no quinto ano, a fábrica produziu 324 itens.
4, _, _, _, 324
Considerando que a razão da PG é igual a q, temos:
4.q4 = 324
q4 = 324/4
q4 = 81
q = 3
Daí, a produção da fábrica foi a seguinte:
Primeiro ano: 4
Segundo ano: 3.4 = 12
Terceiro ano: 3.12 = 36
Quarto ano: = 3.36 = 108
Quinto ano: 324
Total:
4 + 12 + 36 + 108 + 324 = 484
Resposta: E
Questão 4 (Exatus – CFO ES). A largura, a altura e o comprimento de um paralelepípedo reto retângulo formam, nessa ordem, uma progressão geométrica de razão 3. Sabe-se que o volume desse paralelepípedo é igual a 5,832 litros. A altura desse paralelepípedo mede:
a) 1 m
b) 0,5 m
c) 0,23 m
d) 0,18 m
Resolução
Se em 1 metro cúbico temos 1000 litros, para termos 5,832 litros precisamos ter 0,005832 metros cúbicos.
Sabemos que o volume do paralelepípedo é dado pela fórmula: V = largura x altura x comprimento.
Como os lados formam uma PG de razão 3, temos:
Largura = x/3
Altura = x
Comprimento = 3x
Assim,
x/3 . x . 3x = 0,005832
x³ = 0,005832
x = 0,18 m
Resposta: D
Questão 5 (MI – Cespe). Julgue a afirmação abaixo, relativos a sistemas numéricos e sistema legal de medidas.
“A soma 1+ 1/2 + 1/4 + 1/8 + 1/16 + 1/32 é inferior a 2”
Resolução
Claramente temos a soma dos 6 termos de uma PG, onde o primeiro termo é 1 e a razão é 1/2.
Utilizando a fórmula da somados termos de uma progressão geométrica:
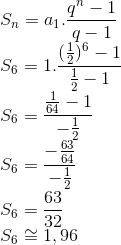
Questão 6 (BASA – Cesgranrio). Considere a sequência numérica cujo termo geral é dado por an=21-3n, para n ≥ 1. Essa sequência numérica é uma progressão
(A) geométrica, cuja razão é -3.
(B) aritmética, cuja razão é 1/8.
(C) geométrica, cuja razão é 1/8.
(D) geométrica, cuja razão é -6.
(E) aritmética, cuja razão é -3.
Resolução
Calculando os primeiros termos da sequência numérica:
a1 = 21-3.1 = 2-2 = 1/4
a2 = 21-3.2 = 2-5 = 1/32
a3 = 21-3.3 = 2-8 = 1/256
Dividindo dois termos consecutivos temos:
a2/a1 = (1/256) / (1/32) = 32/256 = 1/8
a3/a2 = (1/32) / (1/4) = 4/32 = 1/8
Mas será que é sempre igual a 1/8?
Vamos generalizar:
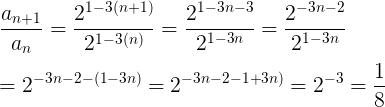
Veja que não importa os termos, a divisão entre dois consecutivos é sempre igual a 1/8, ou seja, temos uma progressão geométrica de razão 1/8.
Resposta: C
Gostou dos nossos exercícios resolvidos sobre progressão aritmética?
Deixe o seu comentário.

Voces sao ótimos!!! Adoro esse site.é o melhor de todos!
Muito obrigado Iana… Você é sempre bem vinda!
Muito bom !!!
Estou gostando muito dessa página !
Obr !
Sou professor de Matemática e Física no Ensino Médio
Agradeço por ter acesso a esse tipo de apoio …
na questao 2, se o sargento tem idade superior a 32, como q ele terá 30 anos???
Fabrício,
O objetivo da questão é verificar se a frase é verdadeira ou falsa.
Ahh ta, nossa não vi o resto da questão hahaha, obg professor
Tmj…