Confira aqui como é possível calcular a probabilidade condicional, onde apresentaremos a definição, a fórmula e alguns exemplos.

Evite pular etapas. O ideal é que o aluno leia primeiro o nosso texto sobre probabilidade, que contém algumas definições e exemplos mais simples.

Bom estudo!

DEFINIÇÃO

Probabilidade condicional é a probabilidade de um evento A ocorrer sabendo que ocorreu o evento B.

A representação é feita por P(A|B), e lida “probabilidade de A acontecer, sabendo que B aconteceu.

Exemplo 1. Calcular a probabilidade de lançarmos dois dados e obtermos a soma igual a 6, sabendo que os lançamentos resultaram em dois números pares.

Temos:

A = soma igual a 6

B = dois números pares

P (A|B) = P (soma igual a 6 | dois números pares)

Agora que aprendemos a definição e a representação da probabilidade condicional, vamos aprender a fórmula matemática utilizada para o cálculo desse tipo de probabilidade.

FÓRMULA MATEMÁTICA DA PROBABILIDADE CONDICIONAL

Dados dois eventos A e B de um determinado espaço amostral, a fórmula utilizada para o cálculo da probabilidade condicional é a seguinte:

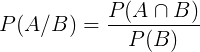
Onde:

P(A|B) = probabilidade de A acontecer, sabendo que B aconteceu

P(A∩B) = probabilidade de A e B acontecerem ao mesmo tempo

P(B) = probabilidade de B acontecer

Agora que aprendemos a fórmula matemática, vamos voltar ao exemplo anterior:

Exemplo 1. Calcular a probabilidade de lançarmos dois dados e obtermos a soma igual a 6, sabendo que os lançamentos resultaram em dois números pares.

Temos:

P(A∩B) = probabilidade da soma ser 6 e os lançamentos resultarem em dois números pares

A probabilidade é calculada através da razão: casos favoráveis / casos possíveis.

O número de casos favoráveis é 2. São eles: 2 + 4, 4 + 2.

O número de casos possíveis é 36. São dois dados e 6 opções para cada, ou seja, 6 x 6.

P(A∩B) = 2 / 36

P(B) = probabilidade dos lançamentos resultarem em números pares

A probabilidade é calculada através da razão: casos favoráveis / casos possíveis.

O número de casos favoráveis é 9. São 3 lados pares em cada dado, ou seja, 3 x 3.

O número de casos possíveis é 36. São dois dados e 6 opções para cada, ou seja, 6 x 6.

P(B) = 9 / 36

Finalizando:

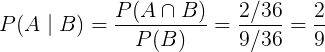
EXEMPLO 2. Uma caixa contém 25 bolas numeradas de 1 a 25. Uma bola é escolhida e percebe-se que o número marcado é maior que 11. Qual é a probabilidade desse número ser múltiplo de 5?

Vamos utilizar a fórmula matemática da probabilidade condicional, onde:

P(A|B) = probabilidade de ser múltiplo de 5, sabendo que é maior que 11

P(A∩B) = probabilidade de ser múltiplo de 5 e maior que 11

P(B) = probabilidade de ser maior que 11

Temos:

Calculando P(A∩B) = P(múltiplo de 5 ∩ maior que 11):

A probabilidade é calculada através da razão: casos favoráveis / casos possíveis.

O número de casos favoráveis é 3. São eles: 15, 20, 25.

O número de casos possíveis é 25. São 25 bolas.

P(A∩B) = 3 / 25

Calculando P(B) = P(maior que 11):

A probabilidade é calculada através da razão: casos favoráveis / casos possíveis.

O número de casos favoráveis é 14 (25 – 11).

O número de casos possíveis é 25. São 25 bolas.

P(B) = 14 / 25

Finalizando:

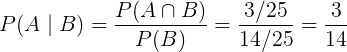
Espero que tenham gostado do nosso conteúdo sobre a probabilidade condicional.

Saber Matemática, o melhor site de matemática para concursos.