Você sabe o que é uma matriz transposta? Veja aqui a definição, as propriedades e vários exemplos.
Bom estudo!
Definição
Dada uma matriz Amxn (m linhas e n colunas), a matriz transposta de A, representada por AT é a matriz que possui os mesmos elementos de A, porém em posições diferentes.
É muito simples: O que é linha se torna coluna e o que é coluna se torna linha.
Exemplo 1:
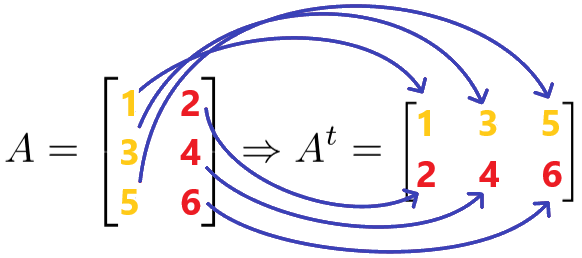
A matriz original possui 3 linhas e 2 colunas.
A matriz transposta possui 2 linhas e 3 colunas.
Exemplo 2:
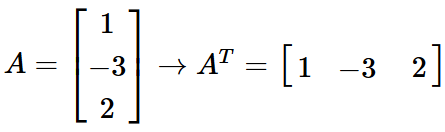
A matriz original possui 3 linhas e 1 coluna.
A matriz transposta possui 1 linha e 3 colunas.
Outra forma de se representar uma matriz inversa é inserindo a letra T no canto superior direito da matriz.
Exemplo 3:
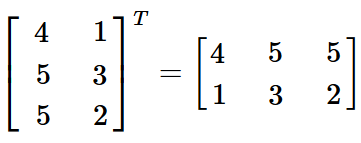
Propriedades da Matriz Transposta
Sejam A e B duas matrizes quaisquer, e x um número real qualquer. As principais propriedades da matriz transposta são as seguintes:
- A transposta da matriz transposta é sempre a matriz original:
(AT)T = A
- A transposta do produto de duas matrizes é o produto das transpostas, com a ordem invertida:
(A.B)T = BT.AT
- A transposta da soma de duas matrizes é a soma das transpostas:
(A + B)T = AT + BT
- A transposta do produto de um número real por uma matriz é o produto do número real pela transposta da matriz:
(x.A)T = x.AT
- O determinante de uma matriz é igual ao determinante da transposta:
det(A) = det(AT)
Aprendeu a calcular a matriz transposta?
Deixe o seu comentário.
