Confira aqui vários exercícios resolvidos sobre os logaritmos, uma matéria que causa muitas dúvidas entre os estudantes.

Lembrando que todos foram retirados de provas de concursos realizados nos últimos anos.

Bom estudo!

Questão 1 (PM ES 2013 – Funcab). Sendo log 2 = 0,30 e log 3 = 0,47, qual o conjunto solução da expressão abaixo?

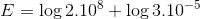
a) S = {6,17}

b) S = {5,33}

c) S = {4,37}

d) S = {3,91}

e) S = {3,77}

Resolução

A questão é relativamente simples para os alunos que já dominam as propriedades dos logaritmos. Veja:

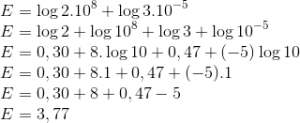
Resposta: E

Questão 2. Qual é o valor da expressão

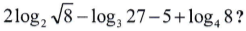
a) 2/7

b) -7/2

c) -2/7

d) 7/2

Resolução

Calcularemos separadamente o valor de cada logaritmo, considerando:

• log₂√8 = x

• log₃27 = y

• log₄8 = z

• Analisando o primeiro logaritmo, temos:

2^x = √8 = 8^1/2 = (2³)^1/2 = 2^3/2

Conclusão: x = 3/2

• Analisando o segundo logaritmo, temos:

3^y = 27 = 3³

Conclusão: y = 3

• Analisando o terceiro logaritmo, temos:

2^2z = 4^z = 8 = 2³

Conclusão: 2z = 3 e z = 3/2

Finalizando:

2.log₂√8 – log₃27 – 5 + log₄8

2.(3/2) – 3 – 5 + 3/2

3 – 3 – 5 + 3/2

-5 + 3/2

-7/2

Resposta: B

Questão 3 (TJ PR 2014). Um investimento rende juros compostos a uma taxa de 6% ao ano. Depois de quantos anos, um valor inicial de R$ 1.000,00 chegará ao valor de R$ 10.000,00 com esse investimento? (Use log(1,06) = 0,025 ).

a) 20 anos.

b) 30 anos.

c) 40 anos.

d) 50 anos.

Resolução

Considerando que o rendimento é através do regime de juros compostos, e utilizando a fórmula para o cálculo do montante, temos:

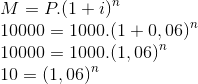
Como temos uma igualdade, vamos utilizar o log em ambos os membros:

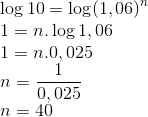
Resposta: C

Questão 4 (TJ SC 2011). Sabendo que log 123 = 2,09, assinale a alternativa que contém o valor de log 1,23.

a) 0,09

b) 0,0209

c) 0,209

d) 1,09

e) 1,209

Resolução

Como log 123 = 2,09, temos:

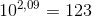
Dividindo ambos os membros por 100:

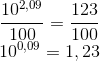
Pela definição de logaritmos:

log 1,23 = 0,09

Resposta: A

Questão 5 (PM Acre – IBADE 2017). A febre amarela é uma doença infecciosa aguda, de curta duração (no máximo 10 dias), gravidade variável, causada pelo vírus da febre amarela, que ocorre na América do Sul e na África. A única forma de evitar a febre amarela silvestre é a vacinação contra a doença. A vacina é gratuita e está disponível nos postos de saúde em qualquer época do ano.

Um posto de saúde iniciou a vacinação contra a febre amarela com um lote de x doses. Sabe-se que o planejado é que o número de doses produzidas dobre a cada ano. Dessa maneira, após quanto tempo esse número passará a ser igual a 20 vezes o inicial? (Use: log2 = 0,3).

a) 4 anos e 4 meses

b) 10 anos e 3 meses

c) 3 anos e 4 meses

d) 4 anos e 1 mês

e) 13 anos e 3 meses

Resolução

Sendo x a quantidade inicial de doses e considerando que o número deve dobrar a cada ano, podemos montar a equação abaixo, onde n é a quantidade de anos.

2ⁿ.x = 20.x

2ⁿ = 20

log(2ⁿ) = log20

n.log2 = log2 + log10

n.0,3 = 0,3 + 1

0,3n = 1,3

n = 1,3/0,3

n = 4,33…

n = 4 anos e 4 meses

Resposta: A

Questão 6 (Vunesp – PM SP). Ao resolver certo problema, encontramos a equação exponencial a^x = 100.

Sabendo que o logaritmo decimal de “a” é igual a 0,54, o valor de “x” é, aproximadamente,

(A) 2,8.

(B) 3,1.

(C) 3,4.

(D) 3,7.

(E) 4,2.

Resolução

Aplicando o logaritmo decimal em ambos os lados da equação:

log(a^x) = log100

x.loga = 2

x.0,54 = 2

x = 2/0,54

x = 3,7

Resposta: D

Questão 7 (PM AL – CESPE). Um corpo com temperatura inicial de 36 °C está em um ambiente cuja temperatura é de 20 °C. Nesse ambiente, vão demorar 20 minutos para que a temperatura inicial do corpo caia para 28 °C. Sabendo-se que o resfriamento de um corpo pode ser modelado pela lei do resfriamento de Newton, conforme a qual a temperatura do corpo T, em função do tempo t, em horas, é dada pela função exponencial T(t) = (T_c−T_a)10^-kt + T_a, em que T_c é a temperatura inicial do corpo e T_a é a temperatura ambiente, é correto afirmar que a constante k é igual a log₁₀(27).

CERTO ou ERRADO?

Resolução

Considerando que 20 minutos é 1/3 de uma hora, podemos utilizar a função exponencial:

T(t) = (T_c − T_a)10^-kt + T_a

28 = (36 − 20)10^-k/3 + 20

28 – 20 = 16.10^-k/3 

8 = 16.10^-k/3 

10^-k/3 = 8/16

10^-k/3 = 1/2

Aplicando log em ambos os lados da igualdade:

log(10^-k/3) = log(1/2)

(-k/3).log10 = log1 – log2

(-k/3).1 = 0 – log2

k/3 = log2

k = 3log2

Resposta: ERRADO

Gostou dos nossos exercícios resolvidos sobre os logaritmos?

Curta e compartilhe nas redes sociais.