Procurando exercícios resolvidos sobre geometria analítica? Chegou ao site certo.
Confira aqui uma seleção especial de questões comentadas, todas retiradas dos últimos concursos públicos realizados pelo país.
Bons estudos.
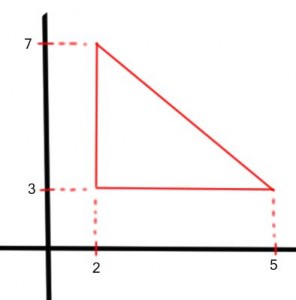
Questão 1 (PM Pará). Os pontos (2,3), (5,3) e (2,7) são vértices de um triângulo retângulo. A área desse triângulo é:
a) 5 u.a
b) 6 u.a
c) 7 u.a
d) 8 u.a
e) 9 u.a
Resolução:
Desenhando o triângulo do plano cartesiano:
Como trata-se de um triângulo retângulo, onde conhecemos a base e a altura, vamos resolver utilizando a fórmula da geometria plana.
b = 5 – 2 = 3
h = 7 – 3 = 4
A = b.h / 2
A = 3.4/2 = 6
Resposta: B
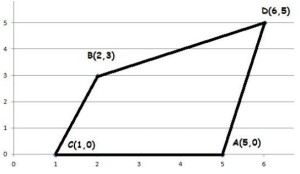
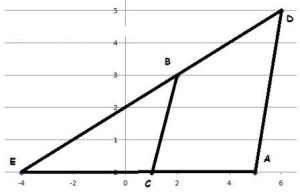
Questão 2 (CFO ES – Exatus). Sendo “S” denominada de área do polígono determinado pelas coordenadas cartesianas dos pontos A(5,0), B(2,3), C(1,0) e D(6,5), qual o valor de S?
a) 15
b) 12
c) 10
d) 28
e) 21
Resolução
Desenhando a figura:
Alongando o lado BD até o eixo x encontramos o ponto E (-4, 0).
A área procurada é a diferença das áreas dos triângulos AED e EBC.
Área do triângulo AED:
A = 9×5/2 = 45/2 = 22,5
Área do triângulo EBC:
A = 5×3/2 = 15/2 = 7,5
Daí, 22,5 – 7,5 = 15
Resposta: A
Questão 3 (PM ES – Exatus). Clarence desenhou o triângulo determinado pelas coordenadas dos pontos cartesianos A(7;5), B(3;2) e C(7;2). Ao calcular a área e o perímetro desse triângulo, os valores obtidos foram, respectivamente:
a) 3 e 3
b) 3 e 6
c) 6 e 6
d) 6 e 12
e) 12 e 12
Resolução
O primeiro passo é marcar os pontos no plano cartesiano e desenhar o triângulo.
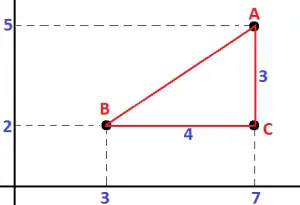
Temos:
ABC é um triângulo retângulo
BC = 4
AC = 3
Descobrindo a medida de AB utilizando o teorema de Pitágoras:
AB² = 4² + 3²
AB² = 16 + 9
AB² = 25
AB = 5
Perímetro = AC + BC + AB
Perímetro = 3 + 4 + 5
Perímetro = 12
Área = b.h/2
Área = 4.3/2
Área = 6
Resposta: D
Questão 4 (PM Paraná – Cops 2010). Considere uma colisão de dois veículos. Num sistema de coordenadas cartesianas, as posições finais destes veículos após a colisão são dadas nos pontos A = (2,2) e B = (4, 1). Para compreender como ocorreu a colisão é importante determinar a trajetória retilínea que passa pelos pontos A e B.
Essa trajetória é dada pela equação:
a) x – y = 0
b) x + y – 5 = 0
c) x – 2y + 2 = 0
d) 2x + 2y – 8 = 0
e) x + 2y – 6 = 0
Resolução
O primeiro passo para entendermos melhor a questão é marcar os pontos e desenhar o segmento de reta.
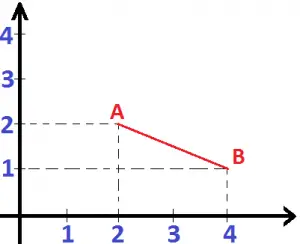
A equação geral da reta que passa por A e B pode ser calculada através da expressão abaixo:
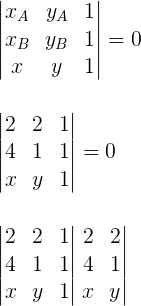
x.1.1 + y.1.2 + 1.4.2 – 2.1.1 – 2.1.x – 1.4.y = 0
x + 2y + 8 – 2 – 2x – 4y = 0
-x – 2y + 6 = 0
x + 2y – 6 = 0
Resposta: E
Questão 5 (UFPR 2013). A figura abaixo apresenta o gráfico da reta r: 2y – x + 2 = 0. no plano cartesiano.
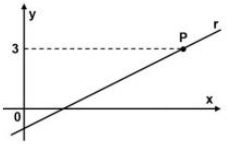
As coordenadas cartesianas do ponto P, indicado nessa figura, são:
a)(3,6).
b)(4,3).
c)(8,3).
d)(6,3).
e)(3,8).
Resolução
Pela figura é possível perceber que a coordenada yP = 3. Nosso objetivo será descobrir o valor de xP.
Como o ponto P pertence à reta r, podemos utilizar a equação geral da reta. Veja:
2y – x + 2 = 0
2yP – xP + 2 = 0
2.3 – xP + 2 = 0
6 – xP + 2 = 0
8 – xP = 0
xP = 8
Resposta: C
Questão 6 (PM AL – CESPE). Em uma cidade, existem três antenas de celular — A, B e C —, representadas em um plano cartesiano de tal forma que A(0, 0), B(2, 0) e C(1/2, √3/2), em que as unidades estão em quilômetros. As antenas A e B captam um telefone celular que está em um ponto P(x0, y0) localizado a 2 km de distância de cada uma delas, e a antena C também recebe sinal desse aparelho. Nesse caso, sabendo-se que y0 > 0, conclui-se que a distância entre P e C é igual a 1 km.
CERTO ou ERRADO?
Resolução
As localizações das três antenas (A, B e C) podem ser representadas em um plano cartesiano.Observe que o telefone celular está em um ponto P, localizado a 2 km de A e B, e como y0 > 0, a figura ABP possui o formato de um triângulo equilátero.
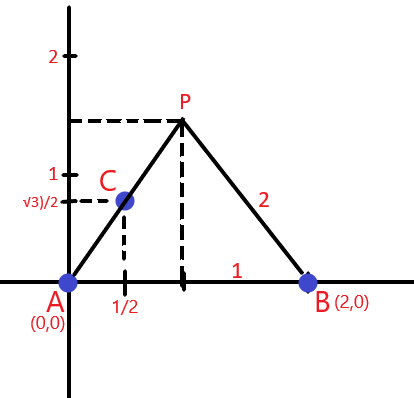
Utilizaremos o Teorema de Pitágoras para calcular a altura h de ABP:
2² = h² + 1²
4 = h² + 1
h² = 4 – 1
h = √3
Observe que A(0,0), C(1/2, √3/2), P(1, √3) são colineares, ou seja, podemos calcular a distância PC através do Teorema de Pitágoras:
PC² = (√3/2)² + (1/2)²
PC² = 3/4 + 1/4
PC² = 4/4
PC² = 1
PC = 1
Resposta: CERTO
Gostou dos nossos exercícios resolvidos sobre geometria analítica?
Curta e compartilhe nas redes sociais.

muito bom o site e os exercicios postados para quem quer estudar engenharia ou arquitetura
Po,muito legal cara gostei mesmo de verdade
olá .. no caso do exercício 2). Na própria figura da para transformar em 2 triângulos e descobrir a área de boa !. Por que alongar ? como fazer isso em uma prova ?
Gostaria de saber por q !
quanto deu o seu ? me ajuda ? como fez ?
Concordo com a afirmação da Andressa…..
soluções sem auxilio de graficos seria o ideal
muito bom não sabe com me ajudou muito,
Obrigada ,do jeito que vc explicou é bem mais fácil de compreender.
Também que me formar para matemática,
estou terminando meu ensino médio.
Obrigado Josiele, que bom que gostou.
Tomara que siga em frente. Tenho certeza que vai se encantar pela matemática.
3) Um navio de massa igual a 1.000 toneladas deve ser rebocado ao longo de um canal estreito por dois tratores que se movem sobre trilhos retos, conforme é mostrado na figura abaixo.
Os tratores exercem forças T1 e T 2 constantes, que têm mesmo módulo, igual a
10.000N, e formam um ângulo de 30 graus com a direção do movimento do navio, representada pela reta AB da figura. Supondo que o navio esteja inicialmente em repouso em relação às margens do canal, calcule:
a) o módulo, a direção e o sentido da aceleração inicial.
Após um determinado intervalo de tempo, com os tratores ainda exercendo força como no início do movimento, a velocidade do navio passa a ser constante, nessas condições, calcule:
b) o módulo, a direção e o sentido da força que a massa de água exerce sobre o navio.
Determine a equação paramétrica da reta r,que passa pelo ponto A(-3,1,0)e P(x,y,z) ponto genérico da reta que possui um vetor diretor v=(3,1,-1).
Por favor me ajudem a resolver essa questão.
Muito interessante as questões abordadas!