Confira aqui as informações mais importantes sobre a função derivada, tudo apresentado de maneira simples e objetiva, para facilitar o entendimento.
Não deixe de ver também as nossas publicações sobre outros tópicos do Cálculo.
Bom estudo!
INTRODUÇÃO
A derivada de uma função f em um ponto xo representa a taxa de variação instantânea de y em relação a x neste ponto xo. Geometricamente, a derivada de uma função em um ponto xo representa a inclinação da reta tangente ao gráfico de f no ponto (xo,f(xo)).

Veja na figura acima que o gráfico da função f está em vermelho e a reta que representa a tangente de f no ponto (xo, f(xo)) está em verde.
DEFINIÇÃO
Seja f: I → R uma função derivável no intervalo aberto I. Podemos definir uma função f‘: I → R que associa todos os valores de I com as suas respectivas derivadas. A função f‘ é chamada de derivada de f.
As principais formas de representação da derivada de uma função f são f‘, df/dx e Df.
A lei da função f‘ pode ser obtida a partir da lei de f, onde devemos aplicar alguns conceitos de limites, a saber:
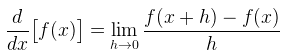

EXEMPLOS
Através da fórmula acima, é possível constatar que:
– Se f(x) = x², f‘(x) = 2x;
– Se f(x) = x³ + 2x, f‘(x) = 3x² + 2;
– Se f(x) = senx, f‘(x) = cosx.
Observação: Apresentamos alguns conceitos básicos para facilitar a compreensão do estudante iniciante. O nosso objetivo foi ser o mais objetivo e o menos formal possível, assim como acontece em todas as publicações do site.
Gostou da nossa publicação sobre a função derivada?
Curta e compartilhe nas redes sociais.
