Confira aqui vários exercícios resolvidos sobre o sólido geométrico prisma, todos retirados de várias provas de concursos realizadas pelo país.

Não deixe de acompanhar também nossos vários conteúdos sobre geometria espacial.

Bom estudo!

 

 

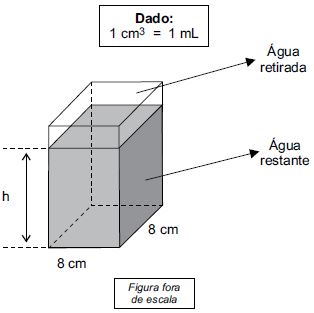
Questão 1 (PM SP – Vunesp 2014). Um recipiente, na forma de um prisma reto de base quadrada, com 8 cm de lado, estava totalmente cheio de água. Desse recipiente foram retirados 160 mL, conforme mostra a figura.

Sabendo que a capacidade máxima desse recipiente é 960 mL, então, após a retirada dos 160 mL, a altura h da água restante dentro dele, em cm, será de

(A) 12,0.

(B) 11,5.

(C) 11,0.

(D) 13,0.

(E) 12,5

 

Resolução

Foi dado que 1 cm³ equivale a 1 ml e que a capacidade máxima do recipiente é de 960 ml, ou seja, 960 cm³.

 

Para calcularmos o volume de um prisma, devemos multiplicar base x lado x altura. Repare que já sabemos o volume, vamos utilizar a fórmula para acharmos a altura:

base x lado x altura = 960

8 x 8 x altura = 960

64 x altura = 960

altura = 960 / 64

altura = 15 cm

 

No sólido geométrico em questão, o volume é proporcional a altura. Vamos calcular em porcentagem quanto o volume foi reduzido:

800/960 = 5/6 (o novo volume é 5/6 do volume total)

 

A altura também deve estar nessa proporção:

15 . 5/6 = 12,5 cm

 

Resposta: E

 

 

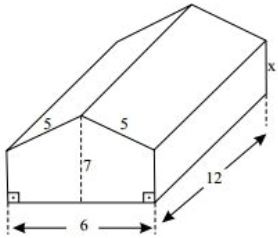
Questão 2 (Sejus ES 2013). Uma tenda de lona foi montada no pátio da penitenciária, com suas medidas em metros e a forma de um prisma reto indicadas na figura. A área total da lona usada na montagem foi 252 m², correspondendo à frente, ao fundo, às laterais e à cobertura.
A altura lateral (x) dessa tenda mede
(A) 3,0 m.

(B) 3,2 m.

(C) 3,5 m.

(D) 2,0 m.

(E) 4,0 m.

 

Resolução

Área das duas laterais, que possuem formato de retângulo (A = base . altura):

2 . 12 . x = 24x

 

Área do teto (2 retângulos):

2 . 5 . 12 = 120

 

Área frente/atrás, onde temos 4 trapézios (a área de um trapézio é o produto da altura pela média das bases:

4 . 3 . (x+7)/2 = 6x + 42

 

Daí,

24x + 120 + 6x + 42 = 252

30x = 252 – 120 – 42

30x = 90

x = 90/30 = 3

 

Resposta: A

 

 

Questão 3 (AFPR – COPS 2013). A figura, a seguir, mostra um pedaço de cartolina que será dobrado e colado ao longo das bordas para formar uma embalagem na forma de um prisma hexagonal regular reto.

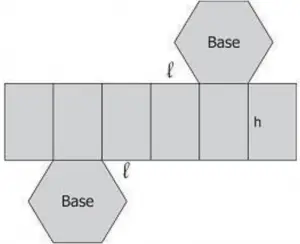
Supondo que l = 2 cm e h = 5 cm, qual é o volume dessa embalagem em cm3?

a) √3  cm³

b) √3/2   cm³

c) 30√3  cm³

d) 6√3  cm³

e) 3√3 cm³

 

Resolução

O volume de um prisma pode ser calculado multiplicando-se a área da base pela altura.

Como a base é um hexágono regular, podemos calcular a área através da seguinte fórmula:

A_b = 3.l².√3/2

A_b = 3.2².√3/2

A_b = 3.4.√3/2

A_b = 6.√3

 

Calculando o volume do prisma:

V = h . A_b

V = 5 . 6.√3

V = 30.√3 cm³

 

Resposta: C

 

 

Espero que gostem dos exercícios resolvidos sobre prisma.

Saber Matemática, o melhor site de matemática para concursos.