Procurando exercícios resolvidos sobre tronco de pirâmide? Confira aqui vários exercícios, todos retirados de provas de concursos.

Não deixe de ver também os exercícios resolvidos sobre os outros tópicos da geometria espacial.

Bom estudo!

 

 

Questão 1 (EsPCEx 2009). Um reservatório em forma de tronco de pirâmide regular de base quadrada e dimensões indicadas na figura deverá ter suas paredes laterais externas cobertas por uma tinta impermeável, cujo rendimento é de 11m² por galão.

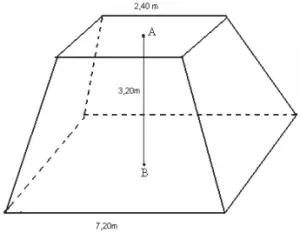
O número mínimo de galões que devem ser adquiridos para tal operação é:

a) 6

b) 7

c) 9

d) 10

e) 11

Nosso objetivo é calcular a área lateral do tronco de pirâmide regular, ou seja, devemos calcular a área de um dos trapézios e multiplicar por 4.

As medidas da base maior e da base menor já foram informadas na figura.

Vamos descobrir a medida da altura dos trapézios.

 

 

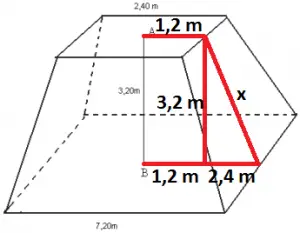
Na figura acima é possível observar que a altura (x) do trapézio pode ser calculada através do Teorema de Pitágoras:

x² = 3,2² + 2,4²

x² = 3,2² + 2,4²

x² = 10,24 + 5,76

x² = 16

x = √16

x = 4 m

 

Calculando a área do trapézio cuja altura, base menor e base maior medem, respectivamente 4 m, 2,4 m e 7,2 m.

 

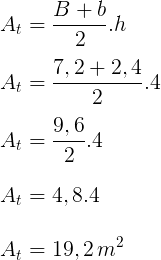
Como cada trapézio possui área de 19,2 m², a área lateral do tronco da pirâmide regular será:

4 . 19,2 = 76,8 m²

 

Se cada galão pinta uma área de 11 m²:

76,8 / 11 = 6,98

 

Daí, são necessários 7 galões.

Resposta: B

 

 

Questão 2 (Escola Naval 2011). As bases de um tronco de pirâmide triangular regular têm de perímetro, respectivamente, 54√3 m e 90√3 m . Se θ é o ângulo formado pela base maior com cada uma das faces laterais e a altura do tronco medindo 6√3m , então tg²θ vale

a) 1/3

b) √3/3

c) 1

d) √3

e) 3

 

Resolução

Trata-se de uma pirâmide regular e triangular, ou seja, as bases do tronco de pirâmide têm formato de triângulos equiláteros. Desta forma, para basta dividir o perímetro por 3 para calcular a medida de cada lado da base. Veja:

54√3 / 3 = 18√3 m

90√3 / 3 = 30√3 m

 

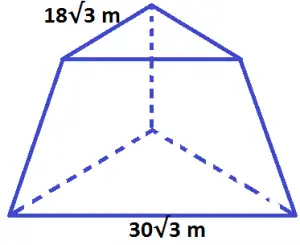
Calculando o apótema dos triângulos equiláteros, bases do tronco de pirâmide:

 

Base superior:

 

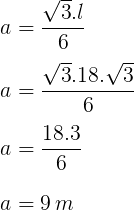
Base inferior:

 

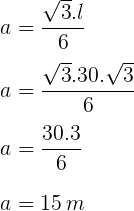
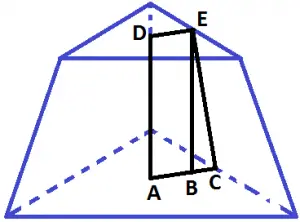
Veja na figura porque calculamos a medida dos apótemas:

 

Veja que:

DE = apótema da base superior

AC = apótema da base inferior

DA = EB = altura do tronco de pirâmide

BC = AC – DE

 

 

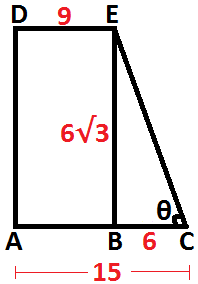
Calculando tgθ:

 

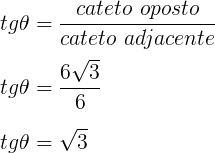
Calculando tg²θ:

tg²θ = (√3)² = 3

 

Resposta: E

 

 

Gostou dos nossos exercícios resolvidos sobre tronco de pirâmide?

Deixe o seu comentário.